まず校訂版にあるように, 式 (11.2) と式 (11.13) とから次式が言えることに注意する:
$
\def\ket#1{|#1\rangle}
\def\bra#1{\langle#1|}
\def\BK#1#2{\langle #1|#2\rangle}
\def\BraKet#1#2#3{\langle#1|#2|#3\rangle}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\odiff#1{\frac{d}{d #1}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2}#1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\mb#1{\mathbf{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
$
\begin{equation*}
\lim_{\beta\to \infty} Z^{'}=e^{-\beta E_{0}^{'}}=\lim_{\beta\to\infty} \int_{-\infty}^{\infty} dx_{1} \int_{x_{1}}^{x_{1}} \mathscr{D}x(u)\,e^{-S^{'}}
=\langle 1 \rangle
\tag{1}
\end{equation*}
この両辺を $C$ について微分する.まず $S^{'}$ は式 (11.61) で与えれているから,
\begin{align*}
\pdiff{C}e^{-S^{'}}&=-e^{-S^{'}}\ppdiff{S^{'}}{C}=-e^{-S^{'}}\frac{1}{2}\int_0^{\beta} dt \int_0^{\beta}ds\,
|\mb{x}(t)-\mb{x}(s)|^{2}\,e^{-w|t-s|}\\
\therefore\quad \pdiff{C}\langle 1 \rangle &=\int \mathscr{D}x(u)\,\pdiff{C}\,e^{-S^{'}}
=\left\langle -\frac{1}{2}\int_0^{\beta} dt \int_0^{\beta} ds\,|\mb{x}(t)-\mb{x}(s)|^{2}\,e^{-w|t-s|}\right\rangle\\
&=-\frac{1}{2}\int_0^{\beta} dt\int_0^{\beta} ds\,|\mb{x}(t)-\mb{x}(s)|^{2}\,e^{-w|t-s|}\,\langle 1 \rangle
\tag{2}
\end{align*}
他方, 左辺を $C$ で微分すると、
\begin{align*}
&\odiff{C}\langle 1 \rangle = \odiff{C}\,e^{-\beta E_0^{'}}=-\beta\,e^{-\beta E_0^{'}}\frac{d E_0^{'}}{dC}
=-\beta\,\langle 1 \rangle\,\frac{d E_0^{'}}{dC},\\
\therefore &\quad \frac{d E_0^{'}}{dC}=-\frac{1}{\beta \langle 1 \rangle}\odiff{C}\langle 1 \rangle
\tag{3}
\end{align*}
以上の式(2) と式(3) 及び前の記事の $B$ の定義から, 直ちに式 (11.78) が得られる:
\begin{equation*}
\frac{d E_0^{'}}{d C}=\frac{1}{2\beta}\int_0^{\beta} dt\int_0^{\beta} ds\,|\mb{x}(t)-\mb{x}(s)|^{2}\,e^{-w|t-s|}=\frac{B}{C}
\tag{11.78}
\end{equation*}
従って, この微分方程式を解くことで $E_0^{'}$ を求めることが出来る.積分する場合に初期条件として $C=0$ のとき$E_0^{'}=0$であることを用いる.
この微分方程式の解法を前述と同様に Mathematica で行なってみるならば, 例えば次となるであろう:
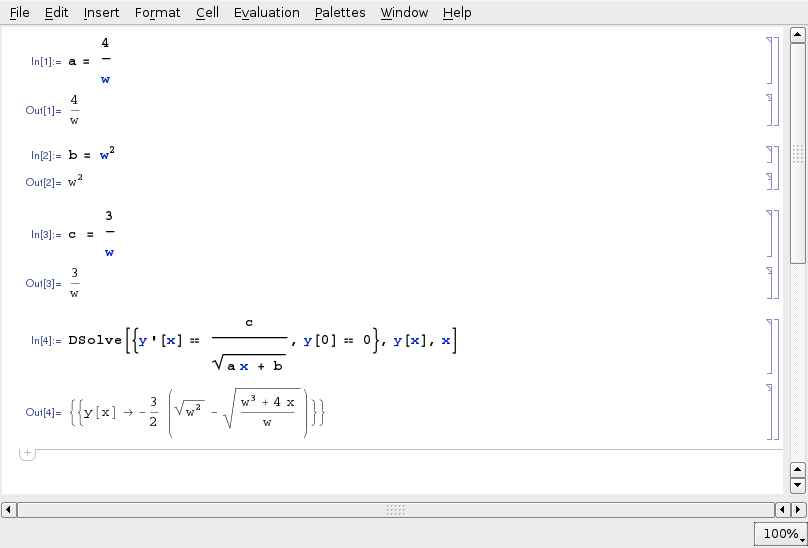
ただし$E_0^{'}\to y$、$C\to x$としてある.すると最後の結果に於いて
\begin{equation*}
\sqrt{\frac{w^{3}+4x}{w}}=\sqrt{w^{2}+\frac{4C}{w}}=v
\end{equation*}
であったことに注意すると, 結局この微分方程式の解 $y[x]$ すなわち $E_0^{'}$ は式 (11.79) に一致していることが分かる:
\begin{equation*}
y[x]\to E_0^{'}=\frac{3}{2}\left(\sqrt{w^{2}+\frac{4C}{w}}\,- w\right)=\frac{3}{2}(v-w)
\tag{11.79}
\end{equation*}
