式(11.77)の$B$を求める

式 (11.77) は式 (11.62) の第 2 項目である $B$ を求めたものである： $$ B=\frac{3C}{v w} \tag{11.77} $$ ファインマンは「$B$ を求める積分は容易に行える」と言っている．論文や本で著者が「この計算は容易に実行出来る」と述べている場面によく出会う．しかし, その場合「この計算は初等的な微積分などの数学公式を用いて解くことが出来るもので, 難解な高等数学公式を用いたり特別な工夫を行う必要はない」という意味に過ぎず「決して計算量が少ないというのではないな！」と思うことがよくある (少ない経験からだけれど)．従って, ときには大量の計算を間違わずに着実に行う必要があるので大変だ．人は計算途中で符号や数値を書き間違えたりしがちだからである．そういう場合にコンピュータで計算結果を検証するのも良いであろう．

そこで式 (11.77) の結果を Mathematica の助けを借りて求めてみよう．

まず式 (11.62) の第 2 項目である $B$ の式を示しておこう： $ \def\ket#1{|#1\rangle} \def\bra#1{\langle#1|} \def\BK#1#2{\langle #1|#2\rangle} \def\BraKet#1#2#3{\langle#1|#2|#3\rangle} \def\ppdiff#1#2{\frac{\partial #1}{\partial #2}} \def\odiff#1{\frac{d}{d #1}} \def\pdiff#1{\frac{\partial}{\partial #1}} \def\Bppdiff#1#2{\frac{\partial^{2}#1}{\partial #2^{2}}} \def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}} \def\mb#1{\mathbf{#1}} \def\ds#1{\mbox{${\displaystyle\strut #1}$}} $

\begin{equation} B=\frac{C}{2\beta}\int_0^{\beta} dt\int_0^{\beta} ds\,\langle | \mathbf{r}(t)-\mathbf{r}(s)|^{2}\rangle\,e^{-w|t-s|} \end{equation}

ここで, 式 (11.76) から

\begin{equation} \langle\,\left| \mb{r}(t)-\mb{r}(s) \right|^{2}\,\rangle = 3\left\{ \frac{4C}{v^{3}w}\left(1-e^{-v|t-s|}\right)+\frac{w^{2}}{v^{2}}|t-s|\right\} \end{equation}

従って式(1) は次となる ：

\begin{align} B&=\frac{3C}{2\beta}\int_0^{\beta} dt\int_0^{\beta} ds\,\left\{ \frac{4C}{v^{3}w}\left(1-e^{-v|t-s|}\right)+\frac{w^{2}}{v^{2}}|t-s|\right\}\,e^{-w|t-s|}\notag\\\ &=\frac{6C^{2}}{v^{3}w}\frac{1}{\beta}\int_0^{\beta} dt\int_0^{\beta} ds\,\left(1-e^{-v|t-s|}\right)\,e^{-w|t-s|} +\frac{3Cw^{2}}{2v^{2}}\frac{1}{\beta}\int_0^{\beta} dt\int_0^{\beta} ds\,|t-s|\,e^{-w|t-s|}\notag\\\ &\equiv \frac{6C^{2}}{v^{3}w}\frac{1}{\beta}I_1 + \frac{3Cw^{2}}{2v^{2}}\frac{1}{\beta}I_2 \end{align}

ただし上式中の $I_1$ と $I_2$ は次のような積分である：

\begin{align} I_1 &= \int_0^{\beta} dt\int_0^{\beta} ds\,\left(1-e^{-v|t-s|}\right)\,e^{-w|t-s|},\\\ I_2&=\int_0^{\beta} dt\int_0^{\beta} ds\,|t-s|\,e^{-w|t-s|} \end{align}

この $I_1$ と $I_2$ の積分を Mathematica によって行うならば, それは例えば次のようになるであろう：

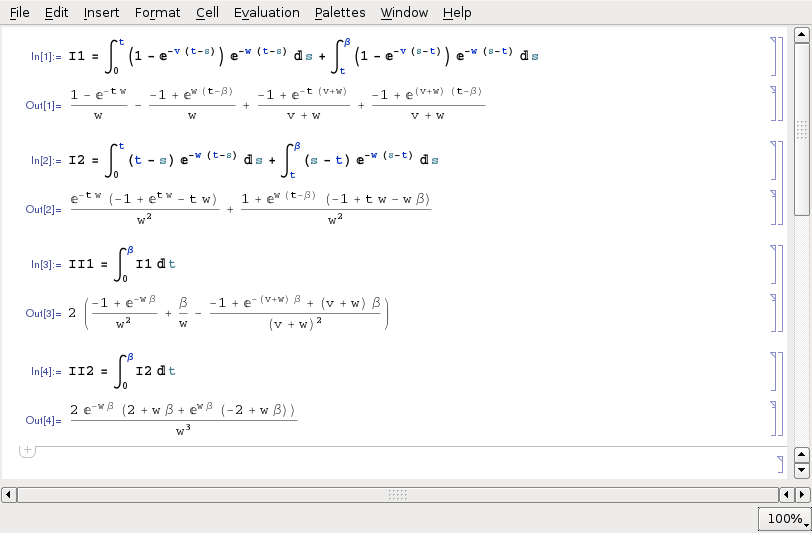
この最終の結果である II1 とII2 を更に簡単化して書くと次となる：

\begin{align} I_1&=2\left(\frac{\beta}{w}-\frac{\beta}{v+w}-\frac{1}{w^{2}}+\frac{1}{(v+w)^{2}}+\frac{e^{-w\beta}}{w^{2}}-\frac{e^{-(v+w)\beta}}{(v+w)^{2}}\right)\\\ I_2&=2\left(\frac{\beta}{w^{2}}+\frac{e^{-w\beta}}{w^{2}}\beta-\frac{2}{w^{3}}+\frac{2\,e^{-w\beta}}{w^{3}}\right) \end{align}

これらの結果を式(3) に代入したものが $B$ である．それを更に簡単化して書くと次となる：

\begin{align} B&=\frac{12C^{2}}{v^{3}w\beta}\left(\frac{\beta}{w}-\frac{\beta}{v+w}-\frac{1}{w^{2}}+\frac{1}{(v+w)^{2}}+\frac{e^{-w\beta}}{w^{2}}-\frac{e^{-(v+w)\beta}}{(v+w)^{2}}\right)\notag\\\ &\quad + \frac{3Cw^{2}}{v^{2}\beta}\left(\frac{\beta}{w^{2}}+\frac{e^{-w\beta}}{w^{2}}\beta-\frac{2}{w^{3}}+\frac{2\,e^{-w\beta}}{w^{3}}\right)\notag\\\ &=\frac{12C^{2}}{v^{3}w}\left(\frac{1}{w}-\frac{1}{v+w}\right)+\frac{3C}{v^{2}}+\mathcal{O}(\beta^{-1}) \label{eqn8} \end{align}

ただし $\beta\to\infty$ の場合にはオーダーが $\beta^{-1}$ 以下の項は無視できる．よって $\beta\to\infty$ の極限では, 式\eqref{eqn8}の最終結果の最初の 2 項だけが残って次となる：

\begin{equation} B=\left\{\frac{12C}{v^{3}w}\left(\frac{1}{w}-\frac{1}{v+w}\right)+\frac{3}{v^{2}}\right\}C \end{equation}

これに $v$ の定義式 (11.74) から得られる $C$, すなわち

\begin{equation} C=\frac{w}{4}(v^{2}-w^{2}) \end{equation}

を代入すると, 最終的に式 (11.77) が得られる：

\begin{equation} B=\left\{\frac{12}{v^{3}w}\cdot\frac{w}{4}(v^{2}-w^{2})\left(\frac{1}{w}-\frac{1}{v+w}\right)+\frac{3}{v^{2}}\right\}C =\frac{3}{v w} C \end{equation}