問題 2-6 の解答例
この問題文は非常に長いので原文よりも訳本の文章を示しておこう．また解答は、T.Jacobson, L.S.Schulman が書いた論文：「Quantum stochastics: the passage from a relativistic to a non-relativistic path integral」を訳したものに, 次の論文
(1). L. H. Kauffman, H.P. Noyes, Discete physics and the Dirac equation, Physics Letters A 218 (1996),
(2). Keith A. Earle, Notes on The Feynman Checkerboard Problem (2011)
などを元に加筆・修正して, この問題に合うようにしたもので代用する．単に自分では解答できなかったからである．
Problem 2-6
経路積分を定義することが出来る汎関数の類は驚くべきほどに色々ある．これまで式(2-15)で与えられるような汎関数を考えてきた．ここで全く異なるタイプを考えよう．このタイプの汎関数は1次元の相対論的運動の問題に現れる．1次元的に運動する粒子が光速で前後にのみ動けるものとする．便宜上, 光速 $c$, 粒子の質量
, プランク定数 $\hbar$ が全て1となるように単位系をとる．そうすると 図2-4 に示すように $x$-$t$ 平面で全ての軌道は $\pm 45$° の傾きで行きつ戻りつする．このような経路の振幅は次のようにして定義される．時間を等しい長さ $\varepsilon$ の小さな区間に分割する．経路の方向転換はこれらの区間の端, 即ち時刻 $t=t_a +n\varepsilon$ ( $n$ は整数 ) に於いてのみ起こるものとする．この相対論的問題について, このような経路に沿っての運動の振幅は式(2-15) で定義される振幅とは異なる．この場合の正しい定義は次である： $$ \phi = (i\epsilon)^{R} \tag{2.26} $$ ここで $R$ は経路に沿っての方向転換の数, 即ち角(corner)の数である．
$\quad$ 問題は以下である： 読者はこの定義を用いて, 1つの角を持つ経路, 2つの角を持つ経路などの寄与の和を取ることにより核 $K(b,a)$ を計算することが出来るであろう．そこで次式を求めよ： $$ K(b,a)=\sum_{R} N(R)\,(i\epsilon)^{R} \tag{2.27} $$ ここで$N(R)$は $R$ 個の角を持つ経路の数である．4個の別々の $K$ を計算するのが良い．即ち, 点 $a$ から負の速度で出発し 点 $b$ に正の速度で到達する振幅 $K_{+-}(b,a)$ などである．$K_{-+}$、$K_{--}$ なども同様に定義される．
$\quad$ 次に時間の単位を
で定義する．時間間隔が非常に長く [$(t_{b}-t_{a})\gg \hbar/mc^{2}$] , 平均速度が小さい [ $x_{b}-x_{a}\ll c(t_{b}-t_{a})$ ] 場合に, 核 (kernel) が 因子 $\exp[(imc^{2}/\hbar)(t_{b}-t_{a})]$ を除いて近似的に自由粒子の核 [ 式(3-3)で与えられる ] と同じであることを示せ．ここで与えられている振幅の定義と求まった核は, 1次元の運動をする自由粒子の相対論的量子力学に於いて正しいものだ．結果はこの場合, Dirac方程式と等価である．
( 解答 )
我々の目標は, 式(2.27)の和への寄与の大部分を起こす方向反転数を見積もることである．そこでまずは, 和 $K_{-+}$ に所属する $R$ 個の屈曲(bend)を持つ経路を考察する．それは右向きに出発し左向きで到着する経路である．その経路は左に $1+(R-1)/2$ 回反転し, 右には $(R-1)/2$ 回の反転をする ( Figure 1. を参照のこと)．
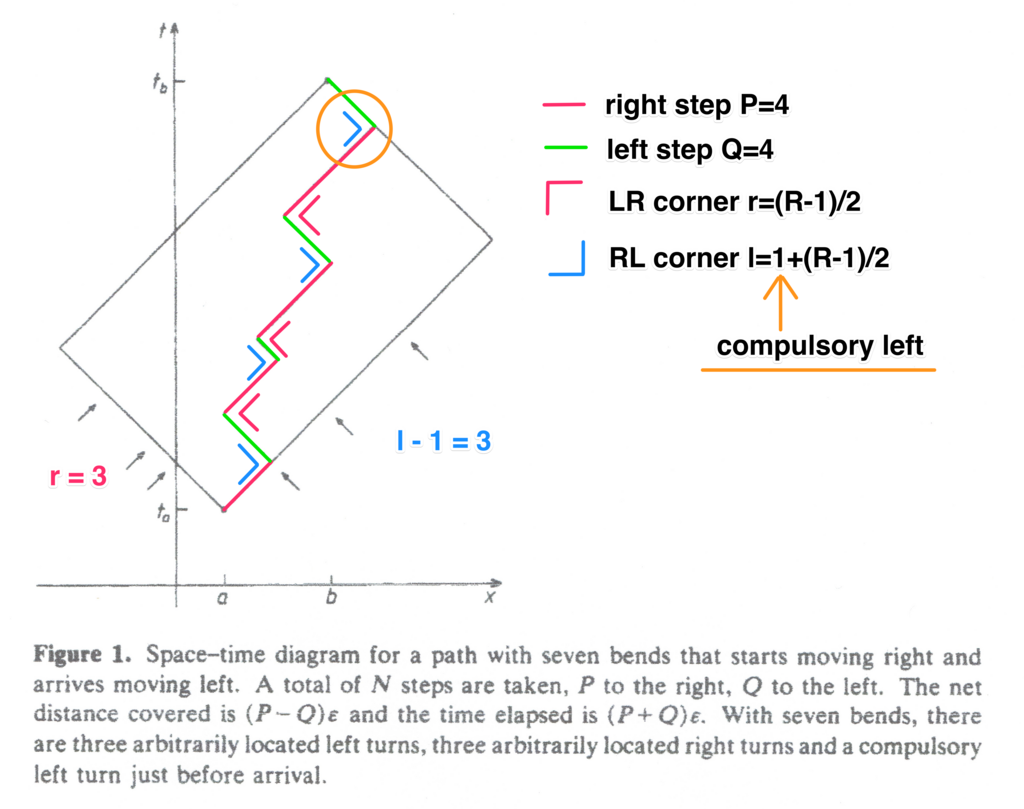
これらの条件を満たすどんな経路も, 矩形領域の左下側の任意位置に $(R-1)/2$ 個の矢印, それは右反転を示す, を配置し, そして右下側には同数の左反転を示す矢印を配置する(1つは強制的に必要なので考慮しない)ことで求めることが出来る．総計で $n$個 のステップがあり, $P$ 個は右ステップで $Q$個 は左ステップであるとしよう．従って, $n=P+Q$ である． そして, 正味の移動距離と時間は次となる： $ \def\ket#1{|#1\rangle} \def\bra#1{\langle#1|} \def\BK#1#2{\langle #1|#2\rangle} \def\BraKet#1#2#3{\langle#1|#2|#3\rangle} \def\ppdiff#1#2{\frac{\partial #1}{\partial #2}} \def\odiff#1{\frac{d}{d #1}} \def\pdiff#1{\frac{\partial}{\partial #1}} \def\Bppdiff#1#2{\frac{\partial^{2}#1}{\partial #2^{2}}} \def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}} \def\mb#1{\mathbf{#1}} \def\ds#1{\mbox{${\displaystyle\strut #1}$}} $
\begin{equation*}
x_b-x_a=(P-Q)\varepsilon\equiv M\varepsilon,\quad t_b-t_a=n\varepsilon=(P+Q)\varepsilon
\end{equation*}
以上から次が言える：
\begin{equation}
P=\frac{1}{2}(n+M),\quad Q=\frac{1}{2}(n-M),\quad -n\le (P-Q)=M\le n=(P+Q).
\tag{1}
\end{equation}
$\quad$ 最後の粒子が矩形の右上に到着する場所(そこでは左反転は強制的に行われるとする)は除外されるので $(P-1)$ 個存在する右向きステップの何処に於いても, 任意に $(R-1)/2$ 個の左反転が可能である．$(R-1)/2$ 個の右反転も $(Q-1)$ 個の左向きステップの任意の位置で出現してよろしい．従って, 組合せの総数を ${}_{n}C_{r}=\left(\begin{array}{@{\,}c@{\,}} n \\ r \end{array}\right)$ と表記するならば,
\begin{equation}
N_{-+}(R) = \left(\begin{array}{@{\,}c@{\,}} P-1 \\ \frac{1}{2}(R-1) \end{array}\right) \left(\begin{array}{@{\,}c@{\,}} Q-1 \\
\frac{1}{2}(R-1) \end{array}\right)
\tag{2}
\end{equation}
なぜなら, 言及した制限を除外すれば, 経路と矢印のばら撒き方には1対1対応があるからである．明らかに、$N_{-+}$ の場合の $R$ は奇数であり, 次が言える：
\begin{equation*}
0\le \frac{1}{2}(R-1) \le \min( P-1, Q-1).
\end{equation*}
$n\to\infty$ の極限では, 式(2.27)の和に寄与するのは, $R/n\to 0$となる$R$の値だけであろう．このことを理解するために, ある $\lambda>0$ を一定値であるとして $R/n=\lambda$ とおこう．$N_{\beta\alpha}(R)< 2^{n}$ であるから,
\begin{equation}
N_{\beta\alpha}(R) (\varepsilon)^{R} < 2^{n}(\varepsilon)^{\lambda n}=\left[ 2\left(\frac{t_b-t_a}{n}\right)^{\lambda}\right]^{n}
\tag{3}
\end{equation}
この最後の表式は $n$ のどんな $n$ のべき乗よりも速やかにゼロに向かう．それに対し和中の各項は $1/n$ でゼロに向かう．$|b-a|<t_b-t_a$ のとき、$P/n$と$Q/n$は$n\to\infty$ の極限で有限に留まる．従って $R/P\to0$ そして $R/Q\to0$ も言える．( $|x_b-x_a|=t_b-t_a$ の場合は屈曲が無いのでまさに一直線である．そのときプロパゲーターは光円錐上の1である)．
$\quad$ $|x_b-x_a|< t_b-t_a$ の場合 (すなわち光円錐の能動的未来圏を進む場合)を考える．[ $P$ は $n$ ステップ中の右向きステップ数で, 粒子の移動距離 $x_b-x_a$ はあまり大きくないと考えられるから大体は $n/2$ 以上である ．それに対して屈曲数 $R$ はゼロから考えて行く数である]．従って $P\gg R$ であるとして
\begin{equation*}
\underbrace{P(P-1)\dotsb (P-\frac{1}{2}(R+3))}_{\frac{1}{2}(R-1)}\ \simeq\ P^{\frac{1}{2}(R-1)}
\end{equation*}
と近似してしまうならば,
\begin{equation}
\left(\begin{array}{@{\,}c@{\,}} P-1 \\ \frac{1}{2}(R-1) \end{array}\right)\simeq \left(\begin{array}{@{\,}c@{\,}} P \\ \frac{1}{2}(R-1) \end{array}\right)\simeq \frac{P^{\frac{1}{2}(R-1)}}{\left(\frac{R-1}{2}\right)!}
\tag{4}
\end{equation}
等号が成り立つのは $n\to\infty$ の極限のときである．この近似がどの程度のものであるかを, 例によって Mathematica で調べてみると, オーダーが同じになる位であると言える：
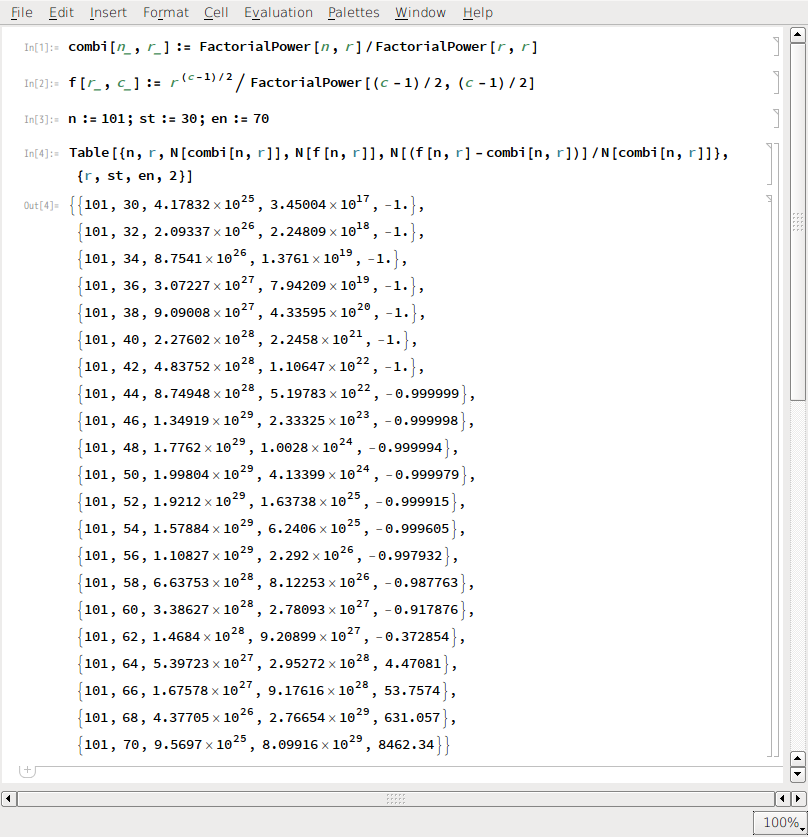
$Q$ の場合にも同様な式が成り立つので, 式(4)と式(2)そして式(2.27)とから次式を得る：
\begin{equation}
K_{-+}=\sum_{\text{odd}\ R} (i\varepsilon)^{R} \frac{(PQ)^{\frac{1}{2}(R-1)}}{\left[\left(\frac{R-1}{2}\right)!\right]^{2}}
\tag{5}
\end{equation}
さてここで, 式(1)から次とおく：
\begin{equation}
PQ=\frac{(n-M)}{2}\frac{(n+M)}{2}=\frac{1}{4}\left(n^{2}-M^{2}\right)=\left(\frac{n}{2}\right)^{2}
\left[1-\left(\frac{M}{n}\right)^{2}\right]=\left(\frac{n}{2\gamma}\right)^{2},
\tag{6}
\end{equation}
ただし,
\begin{equation}
\gamma\equiv \frac{1}{\sqrt{1-v^{2}}} \quad \text{with}\quad v^{2}=\left(\frac{M}{n}\right)^{2}
=\left(\frac{x_b-x_a}{t_b-t_a}\right)^{2}
\tag{7}
\end{equation}
これを式(5)の $N_{-+}$ に用いるならば, そのときの $K$ は,
\begin{equation}
K_{-+}=\sum_{\text{odd}\ R} \left(i\frac{t_b-t_a}{n}\right)^{R}\frac{\frac{2\gamma}{n}\left(\frac{n}{2\gamma}\right)^{R}}{\left[\left(\frac{R-1}{2}\right)!\right]^{2}}=\frac{2\gamma}{n}\sum_{\text{odd}\ R}
\frac{\left(\frac{i(t_b-t_a)}{2\gamma}\right)^{R}}{\left[\left(\frac{R-1}{2}\right)!\right]^{2}}
\tag{8}
\end{equation}
この和は取り得る経路(alternatives)についての総和と解釈することが出来る(これが Feynman が全体の経路積分公式を提示した仕方である)．そして和を構成する各々は, ちょうど $R$ 個の屈曲を持って $x_a$ から $x_b$ へ至る経路に対する確率振幅である．すると最尤の屈曲数 $R_0$ は, その確率振幅が最大の経路を見出すことで見積もることが出来る．この目的のために (to this end)、次とおく：
\begin{align}
z&=\frac{(t_b-t_a)}{\gamma},\quad \text{and,}\quad \exp f(R)\equiv \frac{(z/2)^{R}}{\left[\left(\frac{R-1}{2}\right)!\right]^{2}},
\notag\\
\rightarrow &\quad
f(R)=R\log \frac{z}{2} - 2\log \left(\frac{R-1}{2}\right)! \approx R \log \frac{z}{2} -2\log\left(\frac{R}{2}\right)!
\tag{9}
\end{align}
ここで, 次の「スターリングの近似」を利用しよう：
\begin{equation}
\log n! = n\log n - n +\mathcal{O}(\log n)
\tag{10}
\end{equation}
すると, 上の $f(R)$ は
\begin{equation*}
f(R)\approx R \log \frac{z}{2} -2\left(\frac{R}{2}\log \frac{R}{2}-\frac{R}{2}\right)=R\log\frac{z}{2}-R\log \frac{R}{2}+R
\end{equation*}
$f(R)$ が極値を取るのは, $f(R)$ の微分がゼロのときであると考えられる．即ち,
\begin{equation*}
\ppdiff{f}{R}=\log \frac{z}{2} -\log\frac{R}{2}-R\cdot\frac{2}{R}+1 =\log \frac{z}{2} -\log\frac{R}{2}-1=0
\end{equation*}
の時に最尤確率が生起する．$R\gg 1$ であったから, それはおよそ $R\sim z$ の時と見積もって良いであろう．よって時間の単位を としたことを考慮すれば, 最尤の屈曲数 $R_0$ は,
\begin{equation}
R_0 \sim z=\frac{t_b-t_a}{\gamma}\frac{mc^{2}}{\hbar},\quad\rightarrow\quad R_0 \sim \frac{c(t_b-t_a)}{\lambda_0}
\tag{12}
\end{equation}
そして重大な寄与は, 次を満たす $R$ からである：
\begin{equation}
(R-R_0)^{2} \lesssim \left|\frac{\partial^{2}f}{\partial R^{2}}\right|^{-1}_{R_0} \sim R_0
\tag{13}
\end{equation}
式(12)が示している意味は, 粒子のCompton波長を $\lambda_c=\hbar/mc$ とし粒子の静止系即ち $\gamma_0=1$ の場合で考えるならば「時間 $t=t_b-t_a$ の間に進む距離 $x=c t$ は, 粒子のCompton波長 $\lambda_c$ の $R_0$ 倍であること」 即ち「光速で進む粒子は, 平均するとCompton波長 $\lambda_c$ 毎に方向転換しながら動いている」ということである．
式(12)と式(13)から「屈曲数 $R_0$ は $n$ に依存して増大しないこと, そして粒子の静止系 ( $\gamma=1$ ) に於いては, コンプトン波長 $\lambda_c$ を $c$ で割った時間 $\hbar/mc^{2}$ を単位時間とすると, その単位時間に平均して一つの屈曲が起こる」と結論できる．
式(8)の和は, $n\to\infty$ のとき正確な値となる．ここで奇数の $R$ を $R\equiv 2k+1$ で表す．そして式(5)を $k=\frac{1}{2}(R-1)$ の和と見做し $k\to\infty$ に持って行くならば,
\begin{align}
K_{-+}&=(i\varepsilon)\sum_{k=0}^{\infty} \frac{(i\varepsilon)^{R-1}\left(\frac{n}{2\gamma}\right)^{R-1}}{(k!)^{2}}
=(i\varepsilon)\sum_{k=0}^{\infty} \frac{i^{2k}\left(\frac{n\varepsilon}{2\gamma}\right)^{2k}}{(k!)^{2}}\notag\\
&= i \varepsilon\frac{mc^{2}}{\hbar}\sum_{k=0}^{\infty} (-1)^{k}\frac{(z/2)^{2k}}{(k!)^{2}}
=i \varepsilon\frac{mc^{2}}{\hbar}\, J_0(z)
\tag{14}
\end{align}
ただし $J_0(z)$ はゼロ次のBessel 関数である．
ここで, 点$b$に到達するのは正の速度か負の速度かの2通りあるのだから, 全体を考えるときには場合の数を半分にすべきであろう!?．そこで「更に$1/2$を掛け合わせる」ならば,
\begin{equation}
K_{-+}=\frac{i \varepsilon}{2}\frac{mc^{2}}{\hbar}\sum_{k=0}^{\infty} (-1)^{k}\frac{(z/2)^{2k}}{(k!)^{2}}
=\frac{i \varepsilon}{2}\frac{mc^{2}}{\hbar}\, J_0(z)
\tag{14'}
\end{equation}
他の $K_{\beta\alpha}$ 成分を見積る場合, 因子 $N_{++}$と$N_{--}$ を少し修正する必要がある：
\begin{equation}
N_{++}(R) = \left(\begin{array}{@{\,}c@{\,}} P-1 \\ \frac{1}{2}R \end{array}\right) \left(\begin{array}{@{\,}c@{\,}} Q-1 \\
\frac{1}{2}R-1 \end{array}\right),\quad
N_{--}(R) = \left(\begin{array}{@{\,}c@{\,}} Q-1 \\ \frac{1}{2}R \end{array}\right) \left(\begin{array}{@{\,}c@{\,}} P-1 \\
\frac{1}{2}R-1 \end{array}\right)
\tag{15}
\end{equation}
前と同様な手続きにより, プロパゲーターの 4成分の全てが求まる：
\begin{equation}
K(x,t; 0,0) =\frac{\varepsilon}{2}\frac{mc^{2}}{\hbar} \left(\begin{array}{@{\,}cc@{\,}} K_{++} & K_{+-} \\ K_{-+} & K_{--} \end{array}\right)
= \frac{\varepsilon}{2}\frac{mc^{2}}{\hbar} \left(\begin{array}{@{\,}cc@{\,}} -\frac{t+x/c}{\theta}J_{1}(z) & i J_0(z) \\ i J_0(z) &
-\frac{t-x/c}{\theta}J_1(z) \end{array}\right)
\tag{16}
\end{equation}
ただし $|x|< t$ の場合を考え, また である．
$\quad$上式のようにプロパゲーター $K$ が得られたので, 終時刻 $t_b$ での2成分波動関数は初期時刻 $t_a$ の2成分波動関数から次のように計算できる：
\begin{equation}
\left(\begin{array}{@{\,}c@{\,}} \psi_{R(t_b)} \\ \psi_{L(t_b)} \end{array}\right)
=\frac{\varepsilon}{2}\frac{mc^{2}}{\hbar} \left(\begin{array}{@{\,}cc@{\,}} -\frac{t+x/c}{\theta}J_{1}(z) & i J_0(z) \\ i J_0(z) &
-\frac{t-x/c}{\theta}J_1(z) \end{array}\right)\left(\begin{array}{@{\,}c@{\,}} \psi_{R(t_a)} \\ \psi_{L(t_a)} \end{array}\right)
\tag{17}
\end{equation}
例えば , ここで次の場合を考えてみよう：
\begin{equation}
\psi_{R}(t_{a})=\frac{1}{\sqrt{2}},\quad \psi_{L}(t_{a})=\frac{1}{\sqrt{2}}
\tag{18}
\end{equation}
このとき,
\begin{align}
\psi_{R}(t_{b})&=\frac{\varepsilon}{2}\frac{mc^{2}}{\hbar} \Bigl\{ K_{++}\psi_{R(t_a)}+K_{+-}\psi_{L(t_a)} \Bigr\}\notag\\
&=\frac{\varepsilon}{2\sqrt{2}}\frac{mc^{2}}{\hbar} \left(-\frac{t+x/c}{\theta} J_{1}(z)+i J_0(z)\right)
\tag{19}
\end{align}
ここで Bessel 関数 $J_m(z)$ は, 引数 $z$ の絶対値が大きい場合には次のように近似出来ることを利用する：
\begin{align}
&J_m(z)\approx \sqrt{\frac{2}{\pi z}} \cos\left(z-\frac{2m+1}{4}\pi\right),\quad z\gg 1 \notag\\
&\rightarrow\quad J_0(z)= \sqrt{\frac{2}{\pi z}} \cos\left(z-\frac{\pi}{4}\right),\quad
J_1(z)=\sqrt{\frac{2}{\pi z}} \sin\left(z-\frac{\pi}{4}\right)
\tag{20}
\end{align}
また $t=t_b-t_a,\,x=x_b-x_a$ とすると, 題意の仮定から $t\gg \hbar/mc^{2}$ かつ $x\ll ct$ である．すると式(12)から, その場合の引数 $z$ は次に近似できる：
\begin{equation}
z=\frac{t}{\gamma}\frac{mc^{2}}{\hbar}\approx \frac{mc^{2}t}{\hbar}\sqrt{1-v^{2}/c^{2}}
\approx \frac{mc^{2}t}{\hbar}\left(1-\frac{v^{2}}{2c^{2}}\right)
\tag{21}
\end{equation}
以上を式(19)に適用すると,
\begin{align}
\psi_{R}(t)&\approx \frac{\varepsilon}{2\sqrt{2}}\frac{mc^{2}}{\hbar} \left\{-\gamma\left(1+\frac{v}{c}\right) J_{1}(z)+i J_0(z)\right\}\notag\\
&\approx \frac{i\varepsilon}{2\sqrt{2}} \frac{mc^{2}}{\hbar} \Bigl\{ i J_{1}(z) + J_{0}(z)\Bigr\} \notag\\
&=\frac{i c\varepsilon}{\sqrt{2}}\sqrt{\frac{m}{2\pi\hbar t}}\left\{\cos\left(z-\frac{\pi}{4}\right)
+i\sin\left(z-\frac{\pi}{4}\right)\right\}\notag\\
&= \frac{i c\varepsilon}{\sqrt{2}}\sqrt{\frac{m}{2\pi\hbar t}}\, e^{i(z-\pi/4)}
=\frac{\varepsilon c}{\sqrt{2}} \sqrt{\frac{i m}{2\pi\hbar t}}\,e^{iz}
\tag{22}
\end{align}
このとき, 式(21)から
\begin{equation}
iz\approx \frac{imc^{2}}{\hbar}t -\frac{imv^{2}t}{2\hbar}=\frac{imc^{2}}{\hbar}t -\frac{imx^{2}}{2\hbar t}
\tag{23}
\end{equation}
よって式(22)は,
\begin{equation}
\psi_{R}(t)\approx \frac{\varepsilon c}{\sqrt{2}} \sqrt{\frac{i m}{2\pi \hbar t}}
\exp\left(\frac{imc^{2}}{\hbar}t\right)\exp\left(-\frac{imx^{2}}{2\hbar t}\right)
\tag{24}
\end{equation}
ここで「$n\to\infty$ の時に $\varepsilon c \to 1$ となると仮定し」, 題意にあるように因子 $\exp\left(\frac{imc^{2}}{\hbar}\right)$ を除くと,
\begin{equation}
\psi_{R}(t) \Rightarrow \frac{1}{\sqrt{2}}\sqrt{\frac{i m}{2\pi \hbar t}}\exp\left(-\frac{imx^{2}}{2\hbar t}\right)
\tag{25}
\end{equation}
ここで更に, 変数変換：$t\to -t'$ を行って見よう．すなわち, 「時間反転」をしてみるのである．すると,
\begin{equation*}
\psi_{R}(t')=\frac{1}{\sqrt{2}}\sqrt{\frac{m}{2\pi i\hbar t'}}\exp\left(\frac{imx^{2}}{2\hbar t'}\right)=K_0(b,a)\psi_{R}(t'_a)
\end{equation*}
このとき核は自由粒子の核$K_0(b,a)$に一致したものになった!!．同様にして$\psi_L(t)$からは次も言える：
\begin{equation*}
\psi_{L}(t') = \frac{1}{\sqrt{2}} K_{0}(b,a)=K_{0}(b,a)\psi_{L}(t'_a)
\end{equation*}
2式を一緒にすれば, 2成分スピノールの表現は次となる：
\begin{equation}
\left(\begin{array}{@{\,}c@{\,}} \psi_{R(t'_b)} \\ \psi_{L(t'_b)} \end{array}\right)
=K_0(b,a)\left(\begin{array}{@{\,}c@{\,}} \psi_{R(t'_a)} \\ \psi_{L(t'_a)} \end{array}\right)
\tag{26}
\end{equation}
従って,
『 $n\to\infty$ の時に $\varepsilon c \to 1$ となると仮定し,そして時間反転をするならば, このときの核は「自由粒子核」と同じものとなる．』
が言えると思う!?．[ ちなみに, 修正する前に「空間反転」もして見ると書いてしまったが, その必要はなかった．空間反転に対して, スピノールは反転するが, この自由粒子核は不変であった．]
また Kauffman, Noyes によれば, この場合に $\psi_1$ と $\psi_2$ を次に選ぶならば, その $\psi_1,\,\psi_2$ は前の記事で述べた「$1+1$ Dirac方程式」を満たすようである：
\begin{equation*}
\psi_1 = \sum_{R} (-i)^{R}\Bigl\{ N_{++}(R)+N_{-+}(R) \Bigr\},\quad
\psi_2 = \sum_{R} (-i)^{R}\Bigl\{ N_{+-}(R)+N_{--}(R) \Bigr\}
\end{equation*}
このことは, まだ自分では確かめて居りません!!．
(注)
[1]. 質量 の粒子の「コンプトン波長」は $\lambda_c=h/mc$ と定義される．しかし相対論的量子論では $\lambda_c$を$2\pi$ で割った量も「コンプトン波長」と呼ぶようだ．相対論的量子論では「自然単位系」を念頭にしているからだろうか?．どちらの定義かでその数値も異なるので注意する． 例えば, 電子のコンプトン波長の数値は,
\begin{equation*}
\lambda_e =\frac{h}{mc}=2.426\times 10^{-12} m \ ,\qquad \bar{\lambda}_e=\frac{\hbar}{mc}=\frac{\lambda_e}{2\pi}=3.862\times 10^{-13} m
\end{equation*}
また, J.J.Sakurai : Advanced Quantum Mechanics によれば,「自然単位系」(natural units)とは「作用(エネルギーと時間の積)を $\hbar$ で測り, 長さを時間で割った量を $c$ で計る単位系」である ．
[2]. 次の微分方程式の解をBessel 関数と言う：
\begin{equation*}
\frac{d^{2}y}{dz^{2}}+\frac{1}{z}\frac{dy}{dz}+\left(1-\frac{n^{2}}{z^{2}}\right) y=0
\end{equation*}
この解を特に $J_n(z)$ と書いて「次数$n$の第一種 Bessel 関数」と言う：
\begin{equation*}
J_n(z)=\sum_{m=0}^{\infty} \frac{(-1)^{m}}{m!(n+m)!}\left(\frac{z}{2}\right)^{n+2m}
\end{equation*}
従って,
\begin{equation*}
J_0(z)=\sum_{m=0}^{\infty} \frac{(-1)^{m}}{(m!)^{2}}\left(\frac{z}{2}\right)^{2m},\quad
J_1(z)=\sum_{m=0}^{\infty} \frac{(-1)^{m}}{m!(m+1)!}\left(\frac{z}{2}\right)^{2m+1}
\end{equation*}
例えば, 寺沢貫一著：「自然科学者のための数学概論」の第11章を参照せよ．
[3]. 式(15)の原文の表式には間違いがあることを次の論文に指摘されていた：
[1012.1564] Notes on The Feynman Checkerboard Problem
従って, 式(15)はそれに従って修正したものを示してある．
[4]. 原文では, 式(15)を導出する前で「 $K_{-+}$ は1格子点おきにゼロとなるので, プロパゲーターの連続体近似の表現を得るには $2\varepsilon$ で割る必要がある( Since $K_{-+}$ vanishes at every other lattice point it must be decided by $2\varepsilon$ to obtain the continuum form of the propagator)」と言う文章がある．しかし意味が掴めなかったので, この手続きは省略した．そのために, 式(24)には因子$\varepsilon c$が残ってしまったのである!!．
[5]. 式(4)の近似は, 本質的には ${}_{n}P_{r}$ をスターリングの式により $(n-r)^{r}$ と近似したものを更に $n^{r}$ としてしまうものである．なぜなら, スターリングの式は $n!\simeq n^{n}\,e^{-n}$ とも書けること, そして次の極限の式
\begin{equation*}
\lim_{n\to\infty}\left(1-\frac{r}{n}\right)^{n}=e^{-r}
\end{equation*}
を利用すると, 順列の式が次のように近似できるからである：
\begin{equation*}
{}_n P_r =\frac{n!}{(n-r)!}=\frac{n^{n}\,e^{-n}}{(n-r)^{n-r}\,e^{-(n-r)}}
=\frac{(n-r)^{r}}{\left(1-\frac{r}{n}\right)^{n}}\,e^{-r}\
\xrightarrow{\ n\to\infty\ }\ \frac{(n-r)^{r}}{e^{-r}}\,e^{-r}=(n-r)^{r}
\end{equation*}
