グリーン関数について part 4

以下は, 砂川重信：「理論電磁気学」, 及び J.D.Jackson：「Classical Electrodynamics」, そして ランダウ：「力学・場の理論」から, 関係する部分を抜粋してまとめたものである．ただし Jackson は第３版の訳であるが, そこでの式は, 第10章までは SI単位系 での表現になっているため, このブログで用いている Gauss単位系 に修正してある．因みに第2版までは Gauss単位系 であるようだ．

遅延ポテンシャルと先進ポテンシャル

以下は砂川とJacksonの記述を一緒にしたものである．電磁波がどのようにして発生するかという問題について考えることにする．空間中の電荷分布が激しく変動して, それに伴って周囲の空間の「歪み」つまり電磁場も激しく変動して, それが波動として空間の中を伝搬して行く．この問題を取り扱うためには, 電磁場を記述する最も一般的な Maxwell 方程式から出発しなければならない．

ある決まった電荷と電流の分布がある場合, 場の強さは次の Maxwell-Lorentz の方程式で定まる： $$ \def\BK#1#2{\langle #1|#2\rangle} \def\ppdiff#1#2{\frac{\partial #1}{\partial #2}} \def\odiff#1{\frac{d}{d #1}} \def\pdiff#1{\frac{\partial}{\partial #1}} \def\bppdiff#1#2{\frac{\partial^{2}#1}{\partial #2^{2}}} \def\bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}} \def\mb#1{\mathbf{#1}} \def\ds#1{\mbox{${\displaystyle\strut #1}$}} \text{rot}\,\mb{E}(\mb{x},t)+\frac{1}{c}\ppdiff{\mb{H}(\mb{x},t)}{t}=0,\tag{1} $$ $$ \text{div}\,\mb{H}(\mb{x},t)=0,\tag{2} $$ $$ \text{rot}\,\mb{H}(\mb{x},t)-\frac{1}{c}\ppdiff{\mb{E}(\mb{x},t)}{t}=\frac{4\pi}{c}\mb{j}(\mb{x},t),\tag{3} $$ $$ \text{div}\,\mb{E}=4\pi\rho(\mb{x},t)\tag{4} $$ しかし, ここでの問題の場合には, 電磁ポテンシャル $\mb{A}(\mb{x},t)$ と $\phi(\mb{x},t)$ とを用いた方が便利である：

\begin{equation*} \mb{E}(\mb{x},t)=-\frac{1}{c}\ppdiff{\mb{A}(\mb{x},t)}{t}-\nabla\phi(\mb{x},t),\quad \mb{H}(\mb{x},t)=\text{rot}\,\mb{A}(\mb{x},t),\tag{5} \end{equation*}

このとき式(1)は, 式(5)の第1式の $\mb{E}$ の回転を求めると「全てのグラディエントの回転はゼロである：$\nabla\times\nabla\psi=0$」ことを考慮することで容易に得ることが出来る：

\begin{equation*} \text{rot}\,\mb{E}=\nabla\times\mb{E}=-\frac{1}{c}\pdiff{t}\nabla\times\mb{A}-\underbrace{\nabla\times\nabla\phi}_{=0} =-\frac{1}{c}\pdiff{t}\text{rot}\,\mb{A} =-\frac{1}{c}\ppdiff{\mb{H}}{t} \tag{6} \end{equation*}

また式(2)は, 式(5)の第2式の両辺の発散をとり, $\text{div}\,\text{rot}\,\mb{a}=\nabla\cdot(\nabla\times\mb{a})=0$ を思い起こすと得ることが出来る：

\begin{equation*} \text{div}\,\mb{H}=\text{div}\,\text{rot}\,\mb{A}=\nabla\cdot(\nabla\times\mb{A})=0, \tag{7} \end{equation*}

このとき, 式(3)に式(5)を代入すると,次の関係式が得られる：

\begin{align*} \text{rot}\,\mb{H}(\mb{x},t)-\frac{1}{c}\ppdiff{\mb{E}(\mb{x},t)}{t} &=\nabla\times(\nabla\times\mb{A})-\frac{1}{c}\pdiff{t}\left(-\frac{1}{c}\ppdiff{\mb{A}}{t}-\nabla\phi\right)\\ &=\nabla(\nabla\cdot\mb{A})-\nabla^{2}\mb{A}+\frac{1}{c^{2}}\frac{\partial^{2}\mb{A}}{\partial t^{2}} +\nabla\frac{1}{c}\ppdiff{\phi}{t}\\ &=-\left(\nabla^{2}-\frac{1}{c^{2}}\frac{\partial^{2}}{\partial t^{2}}\right)\mb{A} +\nabla\underbrace{\left(\nabla\cdot\mb{A}+\frac{1}{c}\ppdiff{\phi}{t}\right)}_{=0} =\frac{4\pi}{c}\mb{j} \tag{8} \end{align*}

ここで, ベクトルポテンシャル $\mb{A}$ の任意性から適当な「ゲージ変換」を行って, 第2項目のカッコ内をゼロとすることが出来る．この条件は「Lorentz条件」と呼ばれ, これを満足するポテンシャルを「ローレンツ・ゲージ」のポテンシャルと言う：

\begin{equation*} \nabla\cdot\mb{A}+\frac{1}{c}\ppdiff{\phi}{t}=\text{div}\,\mb{A}+\frac{1}{c}\ppdiff{\phi}{t}=0 \tag{9} \end{equation*}

このとき前式(8)は次となる：

\begin{equation*} \left(\nabla^{2}-\frac{1}{c^{2}}\frac{\partial^{2}}{\partial t^{2}}\right)\mb{A}=-\frac{4\pi}{c}\mb{j} \tag{10} \end{equation*}

また同様にして, 式(4)に式(5)を代入すると, 次の関係式が得られる：

\begin{equation*} \text{div}\,\mb{E}=\nabla\cdot\left(-\frac{1}{c}\ppdiff{\mb{A}}{t}-\nabla\phi\right) =-\frac{1}{c}\pdiff{t}\nabla\cdot\mb{A}-\nabla^{2}\phi=4\pi\rho, \end{equation*}

あるいは,「ローレンツ条件」の式(9)を利用すると次と書くことが出来る：

\begin{equation*} -\frac{1}{c}\pdiff{t}\left(-\frac{1}{c}\ppdiff{\phi}{t}\right)-\nabla^{2}\phi =\frac{1}{c^{2}}\frac{\partial^{2}\phi}{\partial t^{2}}-\nabla \phi =4\pi\rho,\quad \rightarrow\quad \nabla^{2}\phi-\frac{1}{c^{2}}\frac{\partial^{2}\phi}{\partial t^{2}}=-4\pi\rho \tag{11} \end{equation*}

以上の式(10)と式(11)そしてローレンツ条件の式(9)を基本方程式系として採用することが出来る：

\begin{align*} &\left(\nabla^{2}-\frac{1}{c^{2}}\frac{\partial^{2}}{\partial t^{2}}\right)\mb{A}(\mb{x},t) =-\frac{4\pi}{c}\mb{j}(\mb{x},t),\tag{10'}\\ &\left(\nabla^{2}-\frac{1}{c^{2}}\frac{\partial^{2}}{\partial t^{2}}\right)\phi(\mb{x},t) =-4\pi\rho(\mb{x},t),\tag{11'}\\ &\text{div}\,\mb{A}+\frac{1}{c}\ppdiff{\phi(\mb{x},t)}{t}=0\tag{9'} \end{align*}

ただし, 電荷分布 $\rho(\mb{x},t)$ と電流分布 $\mb{j}(\mb{x},t)$とは無限に拡がった真空空間の中のある狭い領域 $V$ にのみ存在するものとし, その値はあらかじめ与えられたものとする．自由電磁波のときはスカラー・ポテンシャル $\phi(\mb{x},t)$ をゼロに選ぶことが出来たが, 今の場合にはそれは出来ない．

波動方程式(10)と式(11)とは次のような基本構造をしていると言える：

\begin{equation*} \nabla^{2}\psi -\frac{1}{c^{2}}\bppdiff{\psi}{t}=-4\pi\,f(\mb{x},t) \tag{12} \end{equation*}

ただし $f(\mb{x},t)$ は既知の源分布である．ファクター $c$ は媒質中の伝搬速度であり, ここでは分散関係はないと仮定する．

式(12)を解くには前ブログ「グリーン関数について part 1」の静電気学の場合と同じく,「グリーン関数」を見出すのが便利である．境界表面のない簡単な状況を考え, 周波数に関するフーリエ変換を導入して明示的な時間依存性を取り除く手続きをする．$\psi(\mb{x},t)$と$f(\mb{x},t)$ のフーリエ積分表現は,

\begin{equation*} \psi(\mb{x},t)=\int_{-\infty}^{\infty} \psi(\mb{x},\omega)\,e^{-i\omega t}\,d\omega,\quad f(\mb{x},t)=\int_{-\infty}^{\infty} f(\mb{x},\omega)\,e^{-i\omega t}\,d\omega \tag{13} \end{equation*}

そして, この逆変換は次となる：

\begin{equation*} \psi(\mb{x},\omega)=\frac{1}{2\pi}\int_{-\infty}^{\infty} \psi(\mb{x},t)\,e^{i\omega t}\,dt,\quad f(\mb{x},\omega)=\frac{1}{2\pi}\int_{-\infty}^{\infty} f(\mb{x},t)\,e^{i\omega t}\,dt \tag{14} \end{equation*}

( 注意) Jacksonの原書では, 規格化因子 $1/2\pi$ が式(13)の方に付けられている．しかし, ここの議論では, 式(14)の逆フーリエ変換の方に付けた方が良いように思われたので修正しておこう!．砂川ではそのようになっている．

式(13)を式(12)に代入すると, フーリエ変換 $\psi(\mb{x},\omega)$ は各々の $\omega$ 値に対して次の「非同次なヘルムホルツ波動方程式」を満たすことが分かる：

\begin{equation*} \bigl(\nabla^{2}+k^{2}\bigr)\psi(\mb{x},\omega)=-4\pi\,f(\mb{x},\omega) \tag{15} \end{equation*}

ただし $k=\omega/c$ は周波数 $\omega$ と関係する波数である．この形では分散がないという制限は必要でない．因果律が幾つかの制限を課すけれども, 先験的には $k$ と $\omega$ の関係は任意でよい．

方程式(15)はポアソン方程式に類似した楕円型偏微分方程式であり, ポアソン方程式は $k=0$ の場合に相当している．式(15)に適した「グリーン関数」$G(\mb{x},\mb{x}')$ は次の非同次方程式を満たすべきである：

\begin{equation*} \bigl(\nabla^{2}+k^{2}\bigr)G_k(\mb{x},\omega)=-4\pi\,\delta(\mb{x}-\mb{x}') \tag{16} \end{equation*}

もし境界表面が存在しないならば, グリーン関数を $\mb{R}=|\mb{x}-\mb{x}'|$ だけに依存するように出来る．また実は, 球対称すなわち$R=|\mb{R}|$ だけに依存するものでなければならない．球座標では,

\begin{align*} &x=r\sin\theta,\quad y=r\sin\theta\sin\phi,\quad z=r\cos\theta\quad r^{2}=x^{2}+y^{2}+z^{2},\quad \tan\theta=\frac{\sqrt{x^{2}+y^{2}}}{z},\quad \tan\phi=\frac{y}{x}\\ &\text{Volume Element: }\ dV=r^{2}dr\sin\theta\,d\theta\,d\phi,\quad\text{Line Element: }\ % ds^{2}=dr^{2}+r^{2}d\theta^{2}+r^{2}\sin^{2}\theta\,d\phi^{2} \end{align*}

この球座標に於けるラプラシアンの形は,

\begin{align*} &\Delta U=\nabla^{2} U=\bppdiff{U}{x}+\bppdiff{U}{y}+\bppdiff{U}{z} =\frac{1}{r^{2}}\pdiff{r}\left(r^{2}\ppdiff{U}{r}\right)+\frac{1}{r^{2}\sin\theta}\pdiff{\theta} \left(\sin\theta\ppdiff{U}{\theta}\right)+\frac{1}{r^{2}\sin^{2}\theta}\bppdiff{U}{\phi}\\ &\quad\text{where}\quad \frac{1}{r^{2}}\pdiff{r}\left(r^{2}\ppdiff{U}{r}\right)=\frac{1}{r}\bpdiff{r} \bigl(r\,U\bigr) \end{align*}

従って, $G_k(R)$ は明らかに次式を満たす：

\begin{equation*} \frac{1}{R}\frac{d^{2}}{dR^{2}}\Bigl(R\,G_k\Bigr)+k^{2}G_k=-4\pi\,\delta(\mb{R}) \tag{17} \end{equation*}

$R=0$ を除いた全ての場所で $R\,G_k(R)$ は次の同次方程式を満たす：

\begin{equation*} \frac{d^{2}}{dR^{2}}\Bigl(R\,G_k\Bigr)+k^{2}\Bigl(R\,G_k\Bigr)=0 \end{equation*}

この解は次とすることが出来る：

\begin{equation*} R\,G_k(R)=A e^{ikR}+B e^{-ikR} \tag{17'} \end{equation*}

それだけでなく, 式(17)中のデルタ関数は $R\to 0$ でのみ影響を与える．その極限では $kR\ll 1$ なので, 方程式はポアソン方程式となる． 従って, 静電気学から正確な規格化は次であることが分かる：

\begin{equation*} \lim_{kR\to0} G_k(R)=\frac{1}{R} \tag{18} \end{equation*}

よって, グリーン関数の一般解は次である：

\begin{equation*} G_k(R)=A\,G_k^{(+)}(R)+B\,G_k^{(-)}(R),\quad\text{where}\quad A+B=1 \tag{19} \end{equation*}

ただし式(17')から $G_k^{\pm}$ は次である：

\begin{equation*} G_k^{(\pm)}(R)=\frac{e^{\pm ikR}}{R} \tag{20} \end{equation*}

式(13)の時間依存についての慣例に従うと, 式(19)の第1項は原点から拡がって行く発散球面波を, そして第2項は収束して行く球面波を表している．

式(19)の $A$ と $B$ の選択は, 物理的問題を特定する「時間の境界条件」に依存する．もし源が, ある時刻 $t=0$ まで静止しており, その後$t>0$ で源が作用し始めるならば, 適切なグリーン関数は源が働き始めた後にそこから外向きに放射される波に相当する式(19)の第1項であることは直感的に明らかである．そのような記述は確かに正確で便利であるが, しかしそれが唯一ではなくまた必然的でもない．境界時間での波の振幅の適切な特定により, 源の作用を記述するのに式(19)の第2項を採用することも可能である!．

$G_k^{(+)}$ と $G_k^{(-)}$ の時間的振る舞いの違いを理解するためには, 相応な「時間依存するグリーン関数」を構築することが必要である．式(12)と, 上述より源は $f(\mb{x},\mb{x}')=\delta(\mb{x}-\mb{x}')\delta(t-t')$ とすればよいことから, その「時間依存するグリーン関数」は次式を満たす：

\begin{equation*} \left(\nabla_x^{2}-\frac{1}{c^{2}}\bpdiff{t}\right)G^{(\pm)}(\mb{x},\mb{x}',t')=-4\pi\delta(\mb{x}-\mb{x}') \delta(t-t') \tag{21} \end{equation*}

従って式(14)を用いれば, 式(15)に相当する源項 $f(\mb{x},\omega)$ は次であることが分かる：

\begin{align*} f(\mb{x},\omega)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}\delta(\mb{x}-\mb{x}')\delta(t-t')\,e^{i\omega t}\,dt =\frac{1}{2\pi}\,\delta(\mb{x}-\mb{x}')\int_{-\infty}^{\infty}\delta(t-t')\,e^{i\omega t}\,dt\\ &=\frac{1}{2\pi}\,\delta(\mb{x}-\mb{x}')\,e^{i\omega t'} \end{align*}

よってこの場合の解は, 式(20)に余分な因子 $e^{i\omega t'}$ が付加されて $G_k^{(\pm)}(R)\,e^{i\omega t'}$ となる．また式(13)から, この場合の $f(\mb{x},t)$ のフーリエ変換は,

\begin{align*} f(\mb{x},t)&=\int_{-\infty}^{\infty} f(\mb{x},\omega)\,e^{-i\omega t}\,d\omega =\int_{-\infty}^{\infty} \frac{1}{2\pi}\,\delta(\mb{x}-\mb{x}')\,e^{i\omega t'}\,e^{-i\omega t}\,d\omega =\frac{1}{2\pi}\int_{-\infty}^{\infty} \delta(\mb{x}-\mb{x}')\,e^{i\omega(t'-t)}\,d\omega \end{align*}

従って, この時間依存する場合では次となるべきである：

\begin{equation*} f(\mb{x},\omega)\to \delta(\mb{R}),\quad\Rightarrow\quad f(\mb{x},\omega)\to \frac{1}{2\pi}\int_{-\infty}^{\infty} \delta(\mb{R})\,e^{i\omega(t'-t)}\,d\omega \end{equation*}

式(16)に対して式(20)の $G_k^{\pm}(R)$ となるのであるから, この場合の式(20)の $G_k^{\pm}(R)$ に相当する「時間依存するグリーン関数」は次となるべきである ：

ただし は式(21)に現れている相対時間である．従って, 無限空間のグリーン関数は源と観測点間の相対距離と相対時間だけの関数である．$k=\omega/c$ の非分散性媒質の場合, 式(22)の積分はデルタ関数である．そのグリーン関数は次となる：

あるいは, より明示的に示すなら $\delta(x)=\delta(-x)$ を用いて次となる：

グリーン関数 $G^{(+)}$ は, 波の擾乱に関する因果的振る舞いを表すことから「遅延グリーン関数」(retarded Green function) と呼ばれている．デルタ関数の引数は, 時刻 $t$ に点 $\mb{x}$ で観測される効果が, 距離$R$ だけ離れた源がそれより以前の時刻 $t'=t-R/c$ に起こった作用に起因することを示している．時間差 $R/c$ はまさに「擾乱が1つの点から他の点へ伝搬する時間」である．同様にして, $G^{(-)}$ は「先進グリーン関数」(advanced Green function)と呼ばれている．

非同次な波動関数である式(12)の特解 (particular integrals) は次である：

\begin{equation*} \psi^{(\pm)}(\mb{x},t)=\iint G^{(\pm)}(\mb{x},t;\mb{x}',t')\,f(\mb{x}',t')\,d^{3}\mb{x}'\,dt' \end{equation*}

ある明確な物理問題を特定するために, このどの積分にも斉次方程式の解を付加することが許される．時間的にも空間的にも局在した源分布$f(\mb{x}',t')$ を考える．これは$t'$ 近傍の僅かな有限時間だけゼロでない．2つの極限状況が想像される(be envisioned)．一つ目の状況では, 時刻 $t\to-\infty$ で同次波動方程式を満たす波 $\psi_{\text{in}}(\mb{x},t)$ が存在すると仮定される．この波は時間と空間の中を伝搬して行く．源が起動するとその源固有の波を発生する．全ての時間のこの状況に対する完全な解は明らかに次である：

\begin{equation*} \psi(\mb{x},t)=\psi_{\text{in}}(\mb{x},t)+\iint G^{(+)}(\mb{x},t;\mb{x}',t')\,f(\mb{x}',t')\,d^{3}\mb{x}'\,dt' \tag{25} \end{equation*}

$G^{(+)}$ の存在は次のことを保証している：「源が起動されていないずっと前の時刻 $t$ では, 積分からの寄与は存在しない」．存在するのは特定な $\psi_{\text{in}}$ だけである．2番目の状況は, 時間がだいぶ経った時刻 $(t\to+\infty)$ に於いて, 波が同次波動方程式の既知解 $\psi_{\text{out}}$ で与えられると言うものである．すると, 全ての時間に対する完全な解は次である：

\begin{equation*} \psi(\mb{x},t)=\psi_{\text{out}}(\mb{x},t)+\iint G^{(-)}(\mb{x},t;\mb{x}',t')\,f(\mb{x}',t')\,d^{3}\mb{x}'\,dt' \tag{26} \end{equation*}

このとき, 先進グリーン関数が「源が停止(shut off)した後, 源からのシグナルは明らかに存在しないこと 」(そのようなシグナルは全て$\psi_{\text{out}}$ に含まれていると仮定する), を保証していることは明らかである．

最も普遍的な物理的状況は, 式(25)に於いて $\psi_{\text{in}}=0$ としたもので記述される．それはときどき, グリーン関数の式(24)を挿入して次のように書かれる：

\begin{equation*} \psi(\mb{x},t)=\int dt'\int d^{3}\mb{x}'\,\frac{\delta\left(t'-\left\{t-\frac{|\mb{x}-\mb{x}'|}{c}\right\}\right)}{|\mb{x}-\mb{x}'|} f(\mb{x}',t')=\int \frac{[f(\mb{x}',t')]_{\text{ret}}}{|\mb{x}-\mb{x}'|}\,d^{3}\mb{x}' \tag{27} \end{equation*}

ただし, カギ括弧 $[\ ]_{\text{ret}}$ は「時刻$t'$は, 遅延した (retarded) 時刻： $t'=t-|\mb{x}-\mb{x}'|/c$ で評価しなければならない」ことを示している．

「有限な」時間での初期値問題および最終問題は,1次元,2次元そして3次元に於いて詳しく研究されている．読者は 「Morse and Feshbach」またはより数学的に扱っている「Hadamard 」の著書を参照するとよいであろう．

波動方程式(10')と(11')に対して遅延解の式(27)を用いるならば次となる：

\begin{align*} &\Phi(\mb{x},t)=\int_{-\infty}^{\infty} dt' \int_{V} d^{3}\mb{x}'\,\frac{\delta\left(t'-\left\{t-\frac{|\mb{x}-\mb{x}'|}{c}\right\}\right)}{|\mb{x}-\mb{x}'|}\,\rho(\mb{x}',t'),\\ &\mb{A}(\mb{x},t)=\frac{1}{c}\int_{-\infty}^{\infty} dt' \int_{V} d^{3}\mb{x}'\,\frac{\delta\left(t'-\left\{t-\frac{|\mb{x}-\mb{x}'|}{c}\right\}\right)}{|\mb{x}-\mb{x}'|}\,\mb{j}(\mb{x}',t') \tag{28} \end{align*}

これらの表式は簡潔に次のように書くことも出来る：

\begin{align*} &\Phi=\int \frac{[\rho(\mb{x}',t')]_{\text{ret}}}{|\mb{x}-\mb{x}'|}\,d^{3}\mb{x}'=\int \frac{\rho_{t-R/c}}{R}\,dV,\\ &\mb{A}=\frac{1}{c}\int \frac{[\mb{j}(\mb{x}',t')]_{\text{ret}}}{|\mb{x}-\mb{x}'|}\,d^{3}\mb{x}' =\frac{1}{c}\int \frac{\mb{j}_{t-R/c}}{R}\,dV \tag{29} \end{align*}

ただし $\mb{R}=\mb{x}-\mb{x}'$ であり, これ以降では $R=|\mb{x}-\mb{x}'|$ でその向きは $\hat{\mb{R}}=\mb{R}/R$ と定義することにする．$R$ は体積要素$dV=d^{3}\mb{x}'$ から「観測点 $\mb{x}$：場のポテンシャルを求めるべき位置」までの距離である．このときの $\Phi$ 及び $\mb{A}$ は「遅延ポテンシャル」と呼ばれる．

リエナール-ヴィーヒェルト(Liénard-Wiechert)のポテンシャル

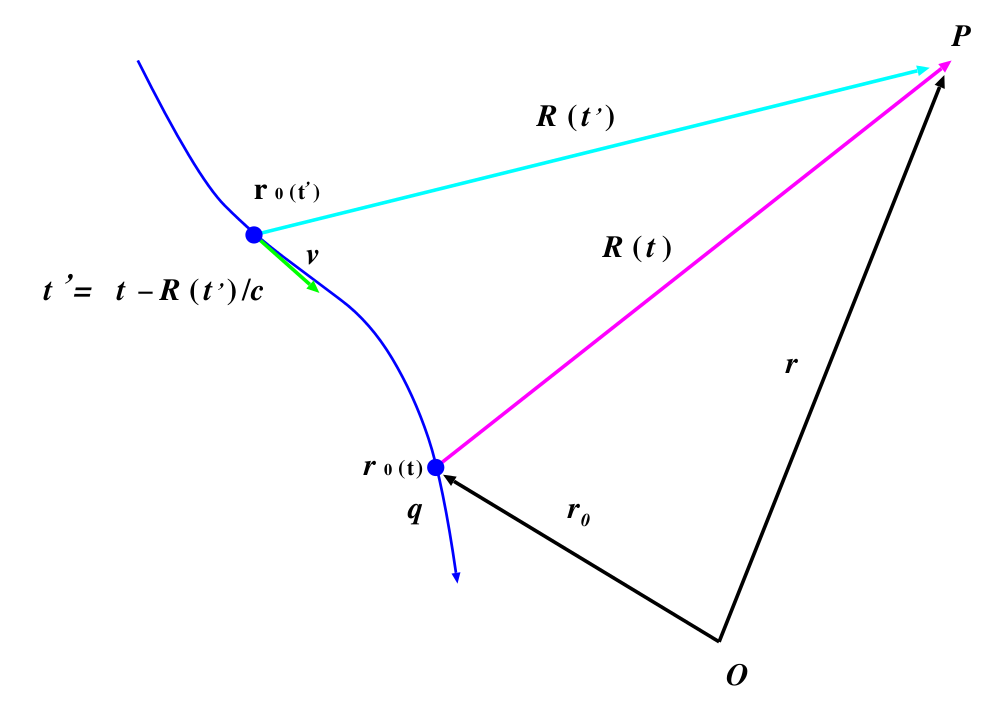
この節はランダウからの抜粋である．「運動している点電荷」によって作られる場のポテンシャルを求めよう．運動の軌道を $\mb{r}_0(t)$ とする．遅延ポテンシャルの公式によると, 時刻$t$ に於ける観測点 $P=\mb{r}$ での場は, それ以前の時刻 $t'$ に於ける電荷の運動状態によって定められる．ここで $t'$ は光の信号が電荷の在る点 $\mb{r}_0(t')$ から観測点 $P$ までの伝播する時間が丁度 $T=t-t'$ に一致するような時刻である．電荷 $q$ から点 $P$ までの動径ベクトルを $\mb{R}(t)=\mb{r}-\mb{r}_0(t)$ とする．これは $\mb{r}_0(t)$と同様に与えられた時間の関数である．そのとき時刻 $t'$ は次の方程式で定められる：

\begin{equation*} t'+\frac{R(t')}{c}=t \tag{30} \end{equation*}

時刻 $t'$ に粒子が静止しているような基準系では, 時刻 $t$ に於ける観測点での場は単にクーロンの法則で与えられる．すなわち,

\begin{equation*} \Phi=\frac{q}{R(t')},\quad \mb{A}=0 \tag{31} \end{equation*}

任意の基準系に於けるポテンシャルの表式を求めるには, 速度 $\mb{v}=0$ で $\Phi$ と $\mb{A}$ が式(31)になるような 4元ベクトルを書けばよい．式(30)によると, 式(31)の $\Phi$ が次の形に書けることに注意する：

\begin{equation*} \Phi=\frac{q}{c(t-t')} \end{equation*}

従って, 求めるべき 4元ベクトルは次であることが分かる：

\begin{equation*} A^{\mu}=q\frac{u^{\mu}}{R_\nu u^{\nu}} \tag{32} \end{equation*}

ただし $u^{\mu}$ は電荷 $q$ の 4元速度

\begin{equation*} u^{\mu}=\left(\gamma,\gamma\frac{\mb{v}}{c}\right) =\left(\frac{1}{\sqrt{1-\beta^{2}}},\frac{\mb{v}}{c\sqrt{1-\beta^{2}}}\right), \quad \text{where}\quad\beta=\frac{v}{c},\quad \gamma=\frac{1}{\sqrt{1-\beta^{2}}} \tag{33} \end{equation*}

であり, また $R^{\mu}$ は次のような 4元ベクトルである：

\begin{equation*} R^{\nu}=\Bigl( c(t-t'),\,\mb{r}-\mb{r}'\Bigr) \tag{34} \end{equation*}

このとき, 式(30)の関係：$t-t'=R/c$ は, 次のような不変な形に書くことが出来る：

\begin{equation*} R_\nu R^{\nu}=c^{2}(t-t')^{2}-(\mb{r}-\mb{r}')^{2}=c^{2}\left(\frac{R}{c}\right)^{2}-R^{2}=0 \tag{35} \end{equation*}

よってこれは不変的な性格のものである．

ここで, 任意の基準系に於ける 4元ベクトル (32)の成分の3次元的な表現に戻ると, 任意の運動をしている点電荷が位置 $P=\mb{r}=(x,y,z)$ に作る場のポテンシャルについて, 次の表式が得られる：

\begin{equation*} \Phi(\mb{r},t)=\left[\frac{q}{\ds{\left(R-\frac{\mb{v}\cdot\mb{R}}{c}\right)}}\right]_{ret},\quad \mb{A}(\mb{r},t)=\left[\frac{q\,\mb{v}}{\ds{c\left(R-\frac{\mb{v}\cdot\mb{R}}{c}\right)}}\right]_{ret} \tag{36} \end{equation*}

ただし $\mb{R}$ は電荷の在る点から観測点 $P$ までの動径ベクトルであり, また「式の右辺にある全ての量には, 式(30)から決まる時刻 $t'$ に於ける値を入れなければ ならない!」ことに注意する．式(36)の形の場のポテンシャルは「リエナール-ヴィーヒェルトのポテンシャル」と呼ばれる．

電場と磁場の強さは次の公式から計算された：

\begin{equation*} \mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t}-\nabla \Phi,\quad \mb{H}=\text{rot}\,\mb{A} \tag{37} \end{equation*}

よって $\Phi$ と $\mb{A}$ を場の点の座標 $(x,y,z)$ と観測時刻 $t$ とについて微分しなければならない．ところが, 公式(36)は $t'$ の関数としてのポテンシャルを式(30)の関係を通して $(x,y,z,t)$ の陰関数として表しているに過ぎない．従って, 求める導関数を計算するには, まず$t'$の微分を計算しておく必要がある．

式(30)または $R(t')=c(t-t')$ という関係を $t$ 及び $\mb{r}$ について微分する．まず $t$ で微分すると,

\begin{equation*} \ppdiff{t'}{t}+\frac{1}{c}\ppdiff{R}{t}=1\quad\rightarrow\quad \ppdiff{R}{t}=c\left(1-\ppdiff{t'}{t}\right) \end{equation*}

次に $\mb{r}$ での微分すなわち $\text{grad}\, R$ を考える．$R(t')=c(t-t')$ を $t'$ で微分すると $$ \ppdiff{R(t')}{t'}=-c $$ となることから, $R$ の微分 $dR$ は次に書ける：

\begin{equation*} dR=\left(\ppdiff{R}{t^{'}}\right)_{\mb{r}} dt'+\left(\ppdiff{R}{\mb{r}}\right)_{t^{'}} d\mb{r},\quad \ppdiff{R}{\mb{r}}=\ppdiff{R}{t^{'}}\ppdiff{t'}{\mb{r}}=-c\ppdiff{t'}{\mb{r}} \quad\rightarrow\quad \ppdiff{R}{\mb{r}}=\left(\ppdiff{R}{t'}\right)_{\mb{r}}\ppdiff{t'}{\mb{r}}+\left(\ppdiff{R}{\mb{r}}\right)_{t'} =-c\ppdiff{t'}{\mb{r}} \end{equation*}

以上から次の結果が得られる：

\begin{equation*} \ppdiff{R}{t}=\ppdiff{R}{t'}\ppdiff{t'}{t}=c\left(1-\ppdiff{t'}{t}\right),\quad \text{grad}\,R =\left(\ppdiff{R}{t'}\right)_{\mb{r}}\,\text{grad}\,t' + \left(\ppdiff{R}{\mb{r}}\right)_{t'}=-c\,\text{grad}\,t' \tag{38} \end{equation*}

また $R^{2}=\mb{R}^{2}$ という恒等式を $t'$ 及び $\mb{r}$ で微分する．$\mb{R}(t)=\mb{r}-\mb{r}_0(t)$ より $\partial\mb{R}/\partial \mb{r}=1$ である．また $\partial \mb{R}(t')/\partial t'=-\mb{v}(t')$ である．ここで負符号が付くのは, $\mb{R}$ が電荷 $q$ から観測点 $P$ への動径ベクトルであり, 速度 $\mb{v}$ は電荷の座標 $\mb{r}_0$ の時間微分であることによる (下図を参照)．$\mb{R}(t')=\mb{r}-\mb{r}_0(t')$ より,

\begin{equation*} \ppdiff{\mb{R}(t')}{t'}=\pdiff{t'}\left\{\mb{r}-\mb{r}_0(t')\right\} =-\pdiff{t'}\mb{r}_0(t')=-\mb{v}(t'). \end{equation*}

以上から,

\begin{equation*} 2R\ppdiff{R}{t'}=2\mb{R}\ppdiff{\mb{R}}{t'}=2\mb{R}\cdot\left(-\mb{v}(t')\right) =-2\mb{R}\cdot\mb{v}(t'),\qquad 2R\ppdiff{R}{\mb{r}}=2\mb{R}\cdot\ppdiff{\mb{R}}{\mb{r}}=2\mb{R} \end{equation*}

よって, 次の結果が得られる：

\begin{equation*} \ppdiff{R}{t'}=-\frac{\mb{R}\cdot\mb{v}}{R},\qquad \ppdiff{R}{\mb{r}}=\frac{\mb{R}}{R} \tag{39} \end{equation*}

この式(39)の結果を式(38)に代入すると次式が得られる：

\begin{equation*} \ppdiff{t'}{t}=\frac{1}{\ds{1-\frac{\mb{R}\cdot\mb{v}}{cR}}},\qquad \text{grad}\,t'=-\frac{\mb{R}}{\ds{c\left(R-\frac{\mb{R}\cdot\mb{v}}{c}\right)}} \tag{40} \end{equation*}

これらの公式を式(36)及び式(37)代入すれば, 場 $\mb{E}$ 及び $\mb{H}$ の計算を遂行することは困難ではない．

[ 逆に言えば,その計算量は大変だと言うことであろう．著者がこう言うときは大抵はそうである． 実は詳しい導出が砂川の第9章の §3 に書かれているので, 興味のある方は参照されたい．ただし, その導出方法は Jackson とは異なっている．時間に余裕があれば, その導出についてまたブログに書いてみるかもしれない．]

途中の計算を省略し, 最終の結果を与えよう．次を定義する：

\begin{equation*} \mb{n}=\frac{\mb{R}}{R},\quad s= R\left(1-\frac{\mb{n}\cdot\mb{v}}{c}\right)\equiv R\kappa,\quad \overrightarrow{\beta}=\frac{\mb{v}}{c},\quad\dot{\mb{v}}=\ppdiff{\mb{v}}{t'} \tag{41} \end{equation*}

このときの $\dot{\mb{v}}$ の定義は, 式(36)で「式の右辺の量はすべて, 時刻$t'$ におけるものであった」ことに由来する．すると場 $\mb{E}$ と $\mb{H}$ の結果は,

\begin{equation*} \mb{E}=\frac{q}{\kappa^{3}R^{2}}\left(1-\overrightarrow{\beta}^{2}\right)\left(\mb{n}-\overrightarrow{\beta}\right) +\frac{q}{c^{2}\kappa^{3}R}\mb{n}\times\left\{\left(\mb{n}-\overrightarrow{\beta}\right)\times\dot{\mb{v}}\right\} \tag{42} \end{equation*}

そして,

\begin{equation*} \mb{H}=\mb{n}\times\mb{E} \tag{43} \end{equation*}

となる．式(43)の形から,「磁場は至る所で電場に垂直である」という興味深い結果が得られることに注意しよう．電場の式(42)は, 異なった性格を持つ2つの部分から成っている．第1項は「粒子の速度だけに依存」し(加速度には拠らない), 大きな距離の所では $1/R^{2}$ のように変化する．第2項は「加速度に依存」し, 大きな距離の所で $1/R$ のように変化する．この第2項は粒子によって放射される電磁波と関連している．

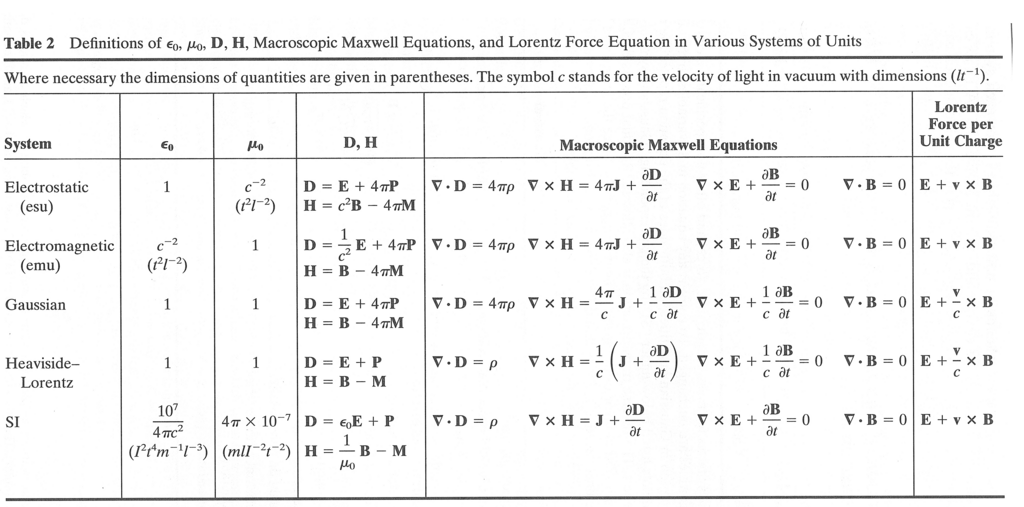
Jacksonの巻末に単位系の換算表があったので, 参考のためにそのコピーを載せておこう．