高校物理でも「ボーアの理論」は学ぶと思う.たとえばある教科書には次のような文章が載っていた:
ラザフォードの原子模型には, 重大な難点があった.従来の電磁波の理論からすると, 原子核の周りの電子の回転運動のために電磁波が放射されるので, 電子はエネルギーを失って行き, 電子の軌道は次第に原子核に近づいて行って, やがて原子核に落ち込んでしまう.
ここの「電磁波の理論」というのは, 例えばランダウ:「力学・場の理論」の第14章「電磁波の放射」に書かれてあり, 何らかの外力作用により荷電粒子が加速度運動すると電磁波が放射されるという理論である.そこには前のブログに書いた「遅延ポテンシャル」や「リエナール - ヴィーヒェルトのポテンシャル」そして「双極放射」などの事柄が載っているわけである.その第4章の § 80 の章末問題に次があった:
問題 5. 一定で一様な磁場の中で円運動を描いて運動する電荷からの放射強度を求めよ.
原子模型の場合とは多少異なるが類似した問題なので, 準備事項をまとめてからこの解答を求めて見よう.
電磁場のエネルギー密度と流れ
以下は, ランダウの § 57 から抜粋してまとめたものである.まずは電気力学の基本方程式であるマクスウェル方程式を示しておく.マクスウェル方程式の第1の組は次である:
$
\def\BK#1#2{\langle #1|#2\rangle}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\odiff#1{\frac{d}{d #1}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\bppdiff#1#2{\frac{\partial^{2}#1}{\partial #2^{2}}}
\def\bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\mb#1{\mathbf{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
$
\begin{equation}
\text{rot}\,\mb{E}=-\frac{1}{c}\ppdiff{\mb{H}}{t},\quad
\text{div}\,\mb{H}=0
\tag{1}
\end{equation}
マクスウェル方程式の第2の組は次である:
\begin{equation}
\text{rot}\,\mb{H}=\frac{1}{c}\ppdiff{\mb{E}}{t}+\frac{4\pi}{c}\mb{j},\quad
\text{div}\,\mb{E}=4\pi \rho
\tag{2}
\end{equation}
式(2)の第1式の両辺に $\mb{E}$ を, そして式(1)の第1式の両辺に $\mb{H}$ を掛け合わせて得られる方程式を組み合わせると次のようになる:
\begin{equation}
\frac{1}{c}\mb{E}\cdot\ppdiff{\mb{E}}{t}+\frac{1}{c}\mb{H}\cdot\ppdiff{\mb{H}}{t}=-\frac{4\pi}{c}\mb{j}\cdot\mb{E}
-(\mb{H}\cdot\text{rot}\,\mb{E}-\mb{E}\cdot\text{rot}\,\mb{H})
\tag{3}
\end{equation}
ここでベクトル解析でよく知られた次の公式を利用して次が言える:
\begin{align}
&\text{div}\,(\mb{a}\times\mb{b})=\nabla\cdot(\mb{a}\times\mb{b})=\mb{b}\cdot\text{rot}\,\mb{a}-\mb{a}\cdot\text{rot}\,\mb{b}\notag\\
&\rightarrow\quad
\text{div}\,(\mb{E}\times\mb{H})=\mb{H}\cdot\text{rot}\,\mb{E}-\mb{E}\cdot\text{rot}\,\mb{H}
\tag{4}
\end{align}
また次が言えることは明らかである:
\begin{align}
&\ppdiff{E^{2}}{t}=\ppdiff{\mb{E}\cdot\mb{E}}{t}=\ppdiff{\mb{E}}{t}\cdot\mb{E}+\mb{E}\cdot\ppdiff{\mb{E}}{t}=2\mb{E}\cdot\ppdiff{\mb{E}}{t}
\notag\\
&\therefore\quad \frac{1}{c}\mb{E}\cdot\ppdiff{\mb{E}}{t}=\frac{1}{2c}\ppdiff{E^{2}}{t}
\tag{5}
\end{align}
これと同様な式が $\mb{H}$ についても言える.以上の式(4)と式(5)とから, 上式(3)は次の形に書き直すことが出来る:
\begin{align}
&\frac{1}{2c}\pdiff{t}\left(E^{2}+H^{2}\right)=-\frac{4\pi}{c}\mb{j}\cdot\mb{E}-\text{div}\,(\mb{E}\times\mb{H})\notag\\
&\text{or}, \quad
\pdiff{t}\left(\frac{E^{2}+H^{2}}{8\pi}\right)=-\mb{j}\cdot\mb{E}-\text{div}\,\mb{S}
\tag{6}
\end{align}
ただしベクトル $\mb{S}$ は次式で定義される「ポインティング・ベクトル」である:
\begin{equation}
\mb{S}\equiv \frac{c}{4\pi}\mb{E}\times\mb{H}
\tag{7}
\end{equation}
式(6)を或る体積について積分し, 右辺の第2項にガウスの定理を適用すると,
\begin{equation}
\pdiff{t}\int \frac{E^{2}+H^{2}}{8\pi}\,dV =-\int \mb{j}\cdot\mb{E}\,dV -\oint \mb{S}\cdot\,d\mb{f}
\tag{8}
\end{equation}
もし積分が全空間に及ぶならば面積積分は消える ( なぜなら場は無限遠ではゼロだからである ).さらに右辺第1項の体積積分は, 全ての電荷についての和 $\sum e\mb{v}\cdot\mb{E}$ と表すことが出来る:
\begin{equation}
\int \mb{j}\cdot\mb{E}\,dV =\sum e\mb{v}\cdot\mb{E}
\tag{9}
\end{equation}
よって次が言える:
\begin{equation}
\pdiff{t}\int \frac{E^{2}+H^{2}}{8\pi}\,dV +\int \mb{j}\cdot\mb{E}\,dV
=\pdiff{t}\int \frac{E^{2}+H^{2}}{8\pi}\,dV +\sum e\mb{v}\cdot\mb{E}=0
\tag{10}
\end{equation}
他方, 粒子の (静止エネルギーも含めた) 運動エネルギー $\mathscr{E}_{\text{kin}}$ の時間変化の割合, すなわち導関数の表式
\begin{equation}
\frac{d\,\mathscr{E}_{\text{kin}}}{dt}=\frac{d}{dt}\left(\frac{m c^{2}}{\sqrt{1-\beta^{2}}}\right),\quad
\text{where}\quad \beta=\frac{v}{c}
\tag{11}
\end{equation}
を求めておく.外力 $\mb{F}$ が粒子に対して仕事 $dW$ をすると, 粒子のエネルギー $E$ はその分だけ増えるから,
\begin{equation}
dE=dW=\mb{F}\cdot d\mb{r}=\frac{d\mb{p}}{dt}\cdot d\mb{r}
\tag{12}
\end{equation}
従って,
\begin{equation}
\frac{d E}{dt}=\frac{d\mb{p}}{dt}\cdot \frac{d\mb{r}}{dt}=\frac{d\mb{p}}{dt}\cdot\mb{v}
\tag{13}
\end{equation}
このとき, 電磁場中の電荷の運動方程式は次に書けた:
\begin{equation}
\frac{d\mb{p}}{dt}=e\mb{E}+\frac{e}{c}\mb{v}\times\mb{H}
\tag{14}
\end{equation}
この右辺の表現は「ローレンツ力」と呼ばれる.
この式(14)を式(13)に代入するならば, $(\mb{v}\times\mb{H})\cdot\mb{v}=0$ となることを考慮して次となる:
\begin{equation}
\frac{d\,\mathscr{E}_{\text{kin}}}{dt}=\frac{d\mb{p}}{dt}\cdot\mb{v}
=\left(e\mb{E}+\frac{e}{c}\mb{v}\times\mb{H}\right)\cdot\mb{v}
=e\mb{v}\cdot\mb{E}
\tag{15}
\end{equation}
よって, この式(15)と式(10)とから,
\begin{align}
&\pdiff{t}\int \frac{E^{2}+H^{2}}{8\pi}\,dV +\sum e\mb{v}\cdot\mb{E}
=\pdiff{t}\int \frac{E^{2}+H^{2}}{8\pi}\,dV +\sum \frac{d\,\mathscr{E}_{\text{kin}}}{dt}\notag\\
&=\frac{d}{dt}\left\{\int \frac{E^{2}+H^{2}}{8\pi}\,dV +\sum \mathscr{E}_{\text{kin}}\right\}=0
\tag{16}
\end{align}
従って, 電磁場とその中に存在する粒子とから成る閉じた系に対して, この方程式の括弧の中の量は保存される.この表式の第2項は全ての粒子の (静止エネルギーを含めた) 運動エネルギーである.従って, 第1項は場自体のエネルギーである.それゆえ, 次の量 $W$ は「電磁場のエネルギー密度」と呼ぶことが出来る:
\begin{equation}
W=\frac{E^{2}+H^{2}}{8\pi}
\tag{17}
\end{equation}
これは「単位体積当たりの場のエネルギー」である.
もし有限な体積について積分するならば, 式(9)の面積積分は消えないから, その方程式を次の形に書くことが出来る:
\begin{equation}
\frac{d}{dt}\left\{\int \frac{E^{2}+H^{2}}{8\pi}\,dV +\sum \mathscr{E}_{\text{kin}}\right\}=-\oint \mb{S}\cdot d\mb{f}
\tag{18}
\end{equation}
ただし, 今度の括弧の中の第2項は「考えている体積内に存在する粒子についてのみ和をとったもの」である.左辺は場と粒子との全エネルギーの単位時間当たりの変化である.従って, 面積分 $\oint \mb{S}\cdot d\mb{f}$ は, 与えられた体積を囲む曲面を横切る場のエネルギーの流れであると解釈されなければならない.それゆえ,「ポインティング・ベクトル $\mb{S}$ は, この流れの密度, すなわち表面の単位面積を単位時間に通過する場のエネルギーの大きさ」なのである.
ここはランダウの §69 からの抜粋である.真空中の電磁波は, 式(1)と式(2)のマクスウェル方程式に於いて$\rho=0$, $\mb{j}=0$ とおくことで決定される:
\begin{align}
&\text{rot}\, \mb{E} = -\frac{1}{c}\ppdiff{\mb{H}}{t},\quad \text{div}\, \mb{H}=0,\tag{19}\\
&\text{rot}\, \mb{H}=\frac{1}{c}\ppdiff{\mb{E}}{t},\quad \text{div}\,\mb{E}=0.
\tag{20}
\end{align}
これらの方程式はゼロでない解を持つので, 電荷の無い場合にも電磁場は存在することが分かる.そのような電磁場は「電磁波」と呼ばれる.なぜなら, 上式より電荷のないときの電磁場は必然的に時間変化するものでなければならないからである.
電磁波のポテンシャルを定める方程式を求める.ポテンシャルには任意性があるので常に付加条件を課すことが可能であった.ここではそれを
「スカラーポテンシャルがゼロである」という条件に選ぼう:$\phi=0$.すると前述したブログ:「グリーン関数について part 4」の, 電磁ポテンシャルで表した電場と磁場の式(5)は次となる:
\begin{equation}
\mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t},\quad \mb{H}=\text{rot}\,\mb{A}.
\tag{21}
\end{equation}
これら2つの表式を式(20)の最初の方程式に代入すると,ベクトル解析の公式:
$\nabla\times(\nabla\times \mb{a})=\nabla(\nabla\cdot\mb{a})-\nabla^{2}\,\mb{a}$ を利用して次となる:
\begin{equation}
\text{rot}\,\text{rot}\,\mb{A}=\text{grad}\,\text{div}\,\mb{A}-\nabla^{2}\,\mb{A}
=\frac{1}{c}\pdiff{t}\left(-\frac{1}{c}\ppdiff{\mb{A}}{t}\right)=-\frac{1}{c^{2}}\bppdiff{\mb{A}}{t}
\tag{22}
\end{equation}
すでにポテンシャルに1個の付加条件:$\phi=0$ を課したけれども, ポテンシャル$\mb{A}$はまだ完全に一義的ではない.すなわち, 時間に依存しない任意関数のグラディエントをそれに加えることが出来る($\phi$はそのまま変えずにおく).とりわけ, 電磁波のポテンシャルを次となるように選べる:
\begin{equation}
\text{div}\,\mb{A}=0
\tag{23}
\end{equation}
これは, 式(21)の第1式を式(20)の第2式に代入すれば分かることである.このとき式(22)より次が得られる:
\begin{equation}
\nabla^{2}\,\mb{A}-\frac{1}{c^{2}}\bppdiff{\mb{A}}{t}=0\quad\text{or}, \quad
\bppdiff{\mb{A}}{t}=c^{2}\left(\bppdiff{\mb{A}}{x}+\bppdiff{\mb{A}}{y}+\bppdiff{\mb{A}}{z}\right)
\tag{24}
\end{equation}
この電磁場のポテンシャルを定める式は「ダランベール方程式」あるいは「波動方程式」と呼ばれる.この式に演算子 $\text{rot}$ および $\partial /\partial t$ を作用させることによって, 電場 $\mb{E}$ および磁場$\mb{H}$ が同じ波動方程式を満たすことが証明される.
平面波の場合
場がただ一つの座標, 例えば $x$ (および時間 $t$ ) にだけ依存するような, 電磁波の特殊な場合を考察する.このような波は「平面波」と呼ばれる.この場合, 場に対する方程式は次となる:
\begin{equation}
\bppdiff{f}{x}-c^{2}\bppdiff{f}{t}=0
\tag{25}
\end{equation}
ただし $f$ はベクトル $\mb{E}$ あるいは $\mb{H}$ の任意の成分を表わす.この方程式を解くために, 次の形に書き直す:
\begin{equation}
\left(\pdiff{t}-c\pdiff{x}\right)\left(\pdiff{t}+c\pdiff{x}\right)f=0,
\tag{26}
\end{equation}
そして新しい変数を導入する:
\begin{equation*}
\varepsilon=t-\frac{x}{c},\quad \theta=t+\frac{x}{c}
\end{equation*}
このとき,
\begin{equation*}
\pdiff{\varepsilon}=\frac{1}{2}\left(\pdiff{t}-c\pdiff{x}\right),\quad
\pdiff{\theta}=\frac{1}{2}\left(\pdiff{t}+c\pdiff{x}\right)
\end{equation*}
従って, $f$ に対する方程式は次となる:
\begin{equation}
\frac{\partial^{2}f}{\partial \varepsilon\,\partial \theta}=0
\tag{27}
\end{equation}
この方程式の解は明らかに次の形を持つ:
\begin{equation}
f=f_1(\varepsilon)+f_2(\theta)=f_1\left(t-\frac{x}{c}\right)+f_2\left(t+\frac{x}{c}\right).
\tag{28}
\end{equation}
ただし $f_1$ 及び $f_2$ は任意な関数である.このとき, $f_1(t-x/c)$ は $x$-軸に沿って正方向に進む平面波を表わし, $f_2(t+x/c)$ は $x$-軸に沿って逆の負の方向に進む波を表わすことは容易に示すことが出来る.前節と同様に $\phi=0$, $\text{div}\,\mb{A}=0$ となるように選ぶならば, 条件 $\text{div}\,\mb{A}=0$ からこの平面波のベクトル・ポテンシャルは常に $x$-軸に垂直すなわち波の伝搬方向に垂直に選ぶことが出来る.
上記の場合の $x$-軸の正方向に進む平面波を考える.この波に於いては, 全ての量, 特に $\mb{A}$ は $t-x/c$ だけの関数である.従って, このときの電場と磁場は次となる:
\begin{align}
&\mb{E}=-\frac{1}{c}\mb{A}^{'},
\tag{29}\\
&\mb{H}=\text{rot}\,\mb{A}=\nabla\times\mb{A}=\nabla\left(t-\frac{x}{c}\right)\times\mb{A}^{'}=-\frac{1}{c}\mb{n}\times\mb{A}^{'}
\notag
\end{align}
ただし「ダッシュは $t-x/c$ についての微分」を表わし, $\mb{n}$ は波の伝搬方向の単位ベクトルである.1番目の式を2番目の式に代入することで次式が得られる:
\begin{equation}
\mb{H}=\mb{n}\times\mb{E},\quad\rightarrow\quad \mb{E}=\mb{H}\times\mb{n}
\tag{30}
\end{equation}
これから, 平面波の電場 $\mb{E}$ と磁場 $\mb{H}$ とは波の伝搬方向に垂直に向いていることが分かる.このために, 電磁波は「横波」と言われる.また上式(30)から「平面波の電場と磁場は互いに直交し等しい大きさを持つ」ことが分かる.
この平面波に於けるエネルギーの流れ即ちポインティング・ベクトルを考える.
ベクトル解析の公式$\mb{a}\times(\mb{b}\times\mb{c})=(\mb{a}\cdot\mb{c})\mb{b}-(\mb{a}\cdot\mb{b})\mb{c}$ 及び, この場合の磁場 $\mb{H}$ はベクトル $\mb{n}$ に直交しているので $\mb{H}\cdot\mb{n}=0$ であることから,
\begin{equation*}
\mb{H}\times(\mb{H}\times\mb{n})=(\mb{H}\cdot\mb{n})\mb{H}-(\mb{H}\cdot\mb{H})\mb{n}=-H^{2}\mb{n}
\end{equation*}
よって式(7)と式(30)とから次が得られる:
\begin{equation}
\mb{S}=\frac{c}{4\pi}\mb{E}\times\mb{H}=\frac{c}{4\pi}(\mb{H}\times\mb{n})\times\mb{H}=-\frac{c}{4\pi}\mb{H}\times(\mb{H}\times\mb{n})=\frac{c}{4\pi}H^{2}\mb{n}
\tag{31}
\end{equation}
立体角要素 $d\Omega$ の中に入る放射の強度 $dI$ は「原点に中心を持つ半径 $R_0$ の球面の要素 $df=R_0^{2}d\Omega$ を単位時間に通過するエネルギー量」と定義される.この量は明らかに「エネルギー流の密度 $S$ に面積要素 $df$ を掛け合わせたもの,すなわち
\begin{equation}
dI=S\,df=c\frac{H^{2}}{4\pi}R_0^{2}\,d\Omega
\tag{32}
\end{equation}
このとき場 $H$ は $R_0$ に反比例するから, 単位時間に立体角要素 $d\Omega$ 内へ系が放射するエネルギー量は, どんな距離に対しても同一である ( 遅延時刻 $t^{'}=t-R_0/c$ の値が同じであるならば ).これは, エネルギーは拡散して行っても消え失せないことから当然なことである.
電荷の系から遠く離れたところの場
運動している電荷の系が生成する場の, その系の大きさに比べて大きな距離を隔てた場所に於ける様子を考察する.座標原点 $O$ を電荷の系の内部の任意点にとる.$O$ から場を定めようとする点 $P$ までの位置ベクトルを $\mb{R}_0$ で表わし, この方向の単位ベクトルを $\mb{n}$ としよう.電荷 $d q=\rho dV$ の動径ベクトルを $\mb{r}$ とし, $d q$ から点 $P$ までの動径ベクトルを $\mb{R}$ とする.
すると, 明らかに $\mb{R}=\mb{R}_0-\mb{r}$ である.
電荷の系から遠いところでは, $R_0\gg r$である.従って, 近似的に次が得られる:
\begin{equation*}
R=|\mb{R}_0-\mb{r}|\approx R_0-\mb{n}\cdot\mb{r}
\end{equation*}
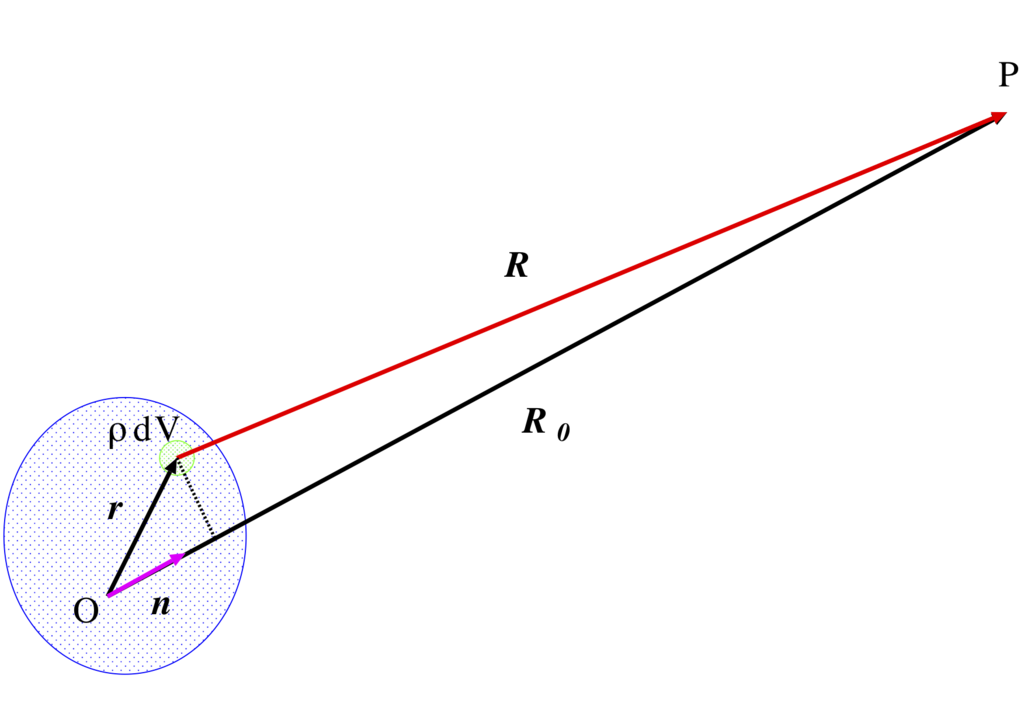
これを遅延ポテンシャルの表式に代入する.被積分関数の分母では, $\mb{r}\cdot\mb{n}$ を $R_0$ に比べて無視できる.しかしながら,
$t-R/c$ に於いてはこれは一般的に許されない.このような項を無視できるか否かは, $R_0/c$と$\mb{r}\cdot\mb{n}/c$ との相対的な値によって決まるのではなく, $\rho$ 及び $\mb{j}$ という量が時間 $\mb{r}\cdot\mb{n}/c$ の間にどれだけ変化するかによって決まるのである.( 遅延ポテンシャルのファインマンの説明を思い出そう ).積分に際して $R_0$ は一定であるから積分の外に出せる.以上から, 電荷系から遠く離れたところでのポテンシャルの表式は次のように近似的に表せる:
\begin{align}
&\phi=\frac{1}{R_0}\int dV\,\rho_{t-R_0/c+\mb{r}\cdot\mb{n}/c}
\tag{33}\\
&\mb{A}=\frac{1}{cR_0}\int dV\,\mb{j}_{t-R_0/c+\mb{r}\cdot\mb{n}/c}
\tag{34}
\end{align}
電荷系から十分に遠く離れたところでは, 空間のあまり大きくない領域範囲で場を平面波と見做すことが出来る.そのためには距離が系の大きさに比べて大きいだけでなく, その系が放射する電磁波の波長に比べても大きいことが必要である.$\mb{r}\cdot\mb{n}/c$ を無視する近似が出来るこのような空間領域を「波動領域 (wave-zone)」または「放射領域 ( radiation-zone)」と呼ぶ.
そこで観測点が波動領域に在り電磁波を平面波と見做せるならば, 場 $\mb{E}$ と $\mb{H}$ とは前節の式(30)が成り立つと言える.すなわち$\mb{E}=\mb{H}\times\mb{n}$.このとき $\mb{H}=\text{rot}\,\mb{A}$ であるから, 波動帯に於ける場を完全に決定するには, ベクトル・ポテンシャル $\mb{A}$ だけを計算すれば十分である.平面波では式(29)より次を得る:
\begin{equation}
\mb{H}=\frac{1}{c}\dot{\mb{A}}\times\mb{n},\quad
\mb{E}=\frac{1}{c}\left(\dot{\mb{A}}\times\mb{n}\right)\times\mb{n}
\tag{35}
\end{equation}
ただし, ドットは遅延時間 $t^{'}=t-R_0/c$ に関する微分を表わす.
式(33)と式(34)から, 遠方に於ける場が, 放射している系からの距離 $R_0$ の1乗に反比例することに注意する.また時間がいつも遅延時刻 $t^{'}=t-R_0/c$ という形で現れることにも注意する.
双極放射
前節の「時間 $\mb{r}\cdot\mb{n}/c$ を無視することが出来る」ための条件を考える.系の電荷分布が著しく変化するのに要する時間の長さの程度を $T$ で表わすと, 系の放射は明らかに $T$ の程度の周期を持つであろう.さらに系の大きさの程度を $a$ で表わすと,
時間 $\mb{r}\cdot\mb{n}/c$ は $a/c$ 程度の大きさである.この時間の間に系の電荷分布が著しい変化を示さないためには $a/c\ll T$ であることが必要である.ところで $cT$ はちょうど放射の波長である.従って条件 $a\ll cT$ は $a\ll \lambda$ という形に書くことが出来る.つまり系の大きさは放射される波の波長に比べて小さいことが必要である.この条件は $v$ が電荷の速度の大きさの程度を表わすとすると $T\sim a/v$ と見積れる.それ故, $\lambda\sim ca/v$ であることに着目すると, さらにもう一つ別の形に書くことが出来る.
すなわち, $a\ll \lambda$ から$v\ll c$ が得られる.従って, 電荷速度は光速度に比べて小さいことが必要である.
以上の条件が満たされていると仮定して, 波長に比べて大きな距離 ( 従って系の大きさに比べて大きな距離 ) だけ系から離れた「波動領域」に於ける放射を考える.( 上述より, このとき我々は非相対論的近似をしていることになるので注意する ).このような距離に於いては, 場は平面波と見做すことが出来て, 場を決定するにはベクトルポテンシャル $\mb{A}$ だけを計算すれば十分であった.遠方に於ける場のベクトルポテンシャルは式(34)より次の形をとる:
\begin{equation}
\mb{A}=\frac{1}{cR_0}\int \mb{j}_{t^{'}}\,dV
\tag{36}
\end{equation}
ただし $t^{'}=t-R_0/c$ である.このとき時間 $t^{'}$ はもはや積分変数には関係しないから, 上式(36)は $\mb{j}=\rho\mb{v}$ を代入することで次の形に書き直すことが出来る:
\begin{equation}
\mb{A}=\frac{1}{cR_0}\int (\rho\,\mb{v})_{t^{'}}\,dV=\frac{1}{cR_0}\sum e\,\mb{v}
\tag{37}
\end{equation}
ただし和は系中の全ての電荷についてとる.そして右辺の全ての量は時間 $t^{'}$ に関するものであるが, 簡略して指標 $t^{'}$ は省いてある.他方, 次であることに注意する:
\begin{equation}
\sum e\,\mb{v}=\frac{d}{dt}\sum e\mb{r} = \dot{\mb{d}}
\tag{38}
\end{equation}
ここで $\mb{d}$ は系の「双極モーメント」である.従って,
\begin{equation}
\mb{A}=\frac{1}{cR_0}\dot{\mb{d}},\quad\rightarrow\quad
\dot{\mb{A}}=\frac{1}{cR_0}\ddot{\mb{d}}.
\tag{39}
\end{equation}
このとき公式(35)を用いると, 磁場と電場は次となる:
\begin{equation}
\mb{H}=\frac{1}{c}\dot{\mb{A}}\times\mb{n}=\frac{1}{c^{2}R_0}\ddot{\mb{d}}\times\mb{n},\quad
\mb{E}=\frac{1}{c^{2}R_0}\left(\ddot{\mb{d}}\times\mb{n}\right)\times\mb{n}
\tag{40}
\end{equation}
今考えている近似では, 放射は系の双極モーメントの2階導関数によって決まることに注意する.この種の放射は「双極放射」と呼ばれる.
このとき $\mb{d}=\sum e\mb{r}$ であるから $\ddot{\mb{d}}=\sum e\dot{\mb{v}}$ である.従って,「電荷は加速度 $\dot{\mb{v}}$ を持って運動するときにのみ放射することが出来る」ことが分かる.
式(40)を式(32)に代入すると, 「双極放射の強度」が得られる:
\begin{equation}
dI=\frac{c}{4\pi}H^{2}R_0^{2}\,d\Omega
=\frac{c}{4\pi}\cdot\frac{1}{\left(c^{2}R_0\right)^{2}}\left(\ddot{\mb{d}}\times\mb{n}\right)^{2}R_0^{2}\,d\Omega
=\frac{1}{4\pi c^{3}}\ddot{\mb{d}}^{2}\,\sin^{2}\theta\,d\Omega
\tag{41}
\end{equation}
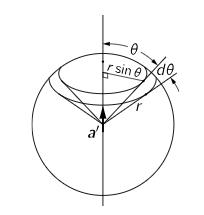
ただし $\theta$ は $\ddot{\mb{d}}$ と $\mb{n}$ の間の角度である.これは「単位時間に系が立体角 $d\Omega$ 内に放射したエネルギー量」である.$d\Omega=2\pi\sin\theta\,d\theta$ と置き ( 下図で $r=1$ とした場合の円帯状の部分に相当する), $\theta$ で $0$ から $\pi$ まで積分する.$t=\cos\theta$ と変数変換して積分を実行すると次の式が得られる:
\begin{equation}
I=\int_0^{\pi}\frac{1}{4\pi c^{3}}\ddot{\mb{d}}^{2}\,\sin^{2}\theta\,2\pi\sin\theta\,d\theta
=\frac{\ddot{\mb{d}}^{2}}{2c^{3}}\int_{-1}^{1}(1-t^{2})\,dt
=\frac{2}{3c^{3}}\ddot{\mb{d}}^{2}
\tag{42}
\end{equation}
外場の中で運動している電荷が1個であれば $\mb{d}=e\mb{r}$ であるから, $\ddot{\mb{d}}=e\ddot{\mb{r}}=e\dot{\mb{v}}$ である.従って, この運動している電荷の放射強度は, 式(42)より次となる:
\begin{equation}
I=\frac{2}{3c^{3}}\ddot{\mb{d}}^{2}=\frac{2}{3c^{3}}(e\dot{\mb{v}})^{2}=\frac{2e^{2}}{3c^{3}}\dot{\mb{v}}^{2}
\tag{43}
\end{equation}
一様で不変な電場および磁場の中の電荷の運動
ここはランダウの § 49 からの抜粋である.一様で不変な電場と磁場の両方が存在するときの電荷の運動を考察する.電荷の速度は小さくて
$v\ll c$ 従って運動量が $\mb{p}=m\mb{v}$ であるような場合に限定する ( このためには電場が磁場に比べて小さいことが必要である ).
磁場 $\mb{H}$ の方向を $z$-軸にとり, $\mb{H}$ と $\mb{E}$ を含む面を $x$-$y$ 面に選ぶ.すると式(14)の運動方程式:
 の各成分の式は, 次の形に書ける:
の各成分の式は, 次の形に書ける:
\begin{equation}
m\ddot{x}=\frac{e}{c}\dot{y}H,\quad m\ddot{y}=eE_y-\frac{e}{c}\dot{x}H,\quad m\ddot{z}=eE_z
\tag{44}
\end{equation}
第3の式から, $z$ 方向には電荷は一定の加速度で運動することが分かる.すなわち,
\begin{equation}
z=\frac{eE_x}{2m} t^{2}+v_{0z}t.
\tag{45}
\end{equation}
また第2の式に虚数単位$i$を掛け, 第1の式と組み合わせると次が見出される:
\begin{equation}
\frac{d}{dt} (\dot{x}+i\dot{y})+i\omega(\dot{x}+i\dot{y})=i\frac{e}{m}E_y, \quad \text{where}\quad \omega=\frac{eH}{mc}
\tag{46}
\end{equation}
この方程式の積分は, この式で右辺がゼロのときの積分 $ae^{-i\omega t}$ と, 右辺があるときの特殊解 $cE_y/H$ との和で与えられ, 次となる:
\begin{equation*}
\dot{x}+i\dot{y}=a\,e^{-i\omega t} +\frac{cE_y}{H}.
\end{equation*}
ただし定数 $a$ は一般に複素数であるが, 位相を適当に選ぶことで $\dot{x}$ と $\dot{y}$ は
\begin{equation}
\dot{x}=a\cos\omega t+ \frac{cE_y}{H},\quad \dot{y}=-a\sin\omega t
\tag{47}
\end{equation}
となり, 粒子の速度は時間の周期関数であることが分かる.この式(47)をもう一度積分して, $t=0$ で $x=y=0$ となるように積分定数を選べば次が得られる:
\begin{equation}
x=\frac{a}{\omega}\sin\omega t +\frac{cE_y}{H}t,\quad
y=\frac{a}{\omega}(\cos\omega t -1)
\tag{48}
\end{equation}
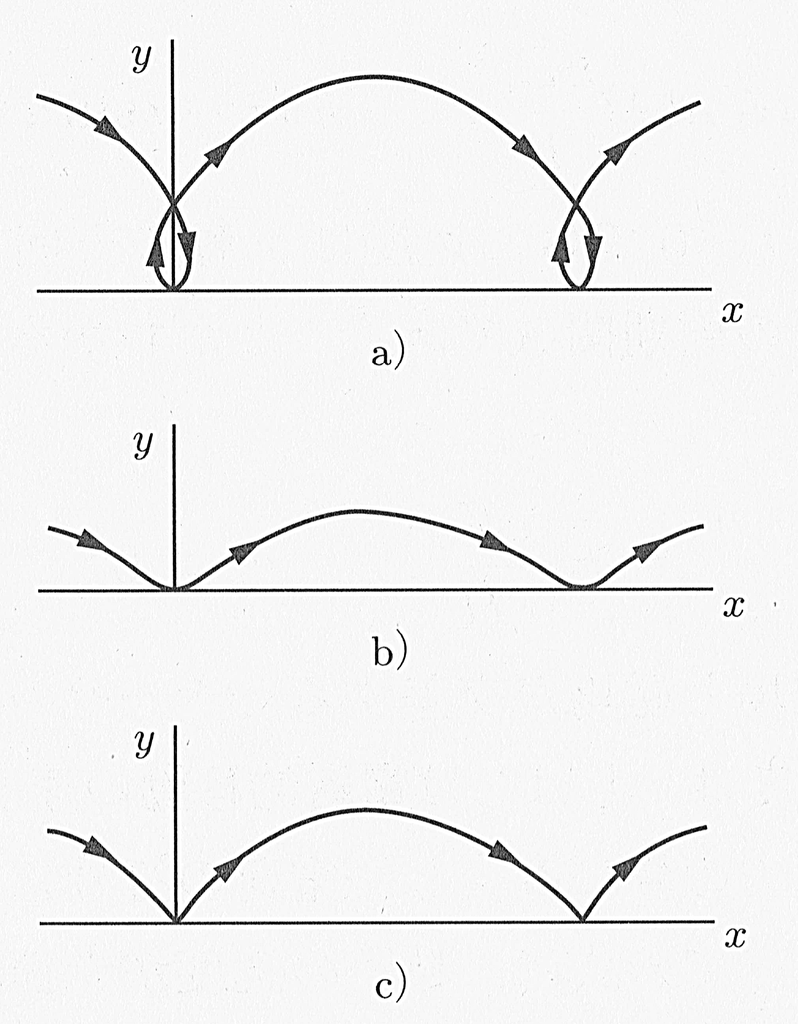
これを曲線のパラメータ表示と見れば, これらの式は「トロコイド」と呼ばれる曲線を与える.$a$ が絶対値に於いて$cE_y/H$ より大きいか小さいかによって, トラジェクトリーの$x$-$y$ 面への射影は下図に示すような形になる:
解答例
以上の事柄を元に, 最初に示したランダウの章末問題に解答してみよう.電場 $\mb{E}$ が存在しない場合を考えると, 運動方程式(44)は次となる:
\begin{align}
&\ppdiff{\,\mb{p}}{t}=m\dot{\mb{v}}=\frac{e}{c}\mb{v}\times\mb{H},\quad\rightarrow\quad
\dot{\mb{v}}=\frac{e}{mc}\mb{v}\times\mb{H},\tag{49}\\
&m\ddot{x}=\frac{e}{c}\dot{y}H,\quad m\ddot{y}=-\frac{e}{c}\dot{x}H,\quad \ddot{z}=0.
\tag{50}
\end{align}
そして式(45)と式(48)は次のような $x$-$y$ 面上の円運動の式とすることが出来る:
\begin{equation}
z=0,\quad x=\frac{a}{\omega}\sin\omega t,\quad y=\frac{a}{\omega}\cos\omega t
\tag{51}
\end{equation}
ただしその円運動の角周波数は $\omega=eH/mc$ である.このとき, 速度ベクトル $\mb{v}$ は $z$-方向の磁場 $\mb{H}$ とは直交する.式(49)の加速度 $\dot{\mb{v}}$ を, 式(43)の放射強度の式に代入するならば,
\begin{equation}
I=\frac{2e^{2}}{3c^{3}}\dot{\mb{v}}^{2}=\frac{2e^{2}}{3c^{3}}\left(\frac{e}{mc}\mb{v}\times\mb{H}\right)^{2}
=\frac{2e^{2}}{3c^{3}}\left(\frac{e}{mc}\right)^{2}|\mb{v}\times\mb{H}|^{2}
\tag{52}
\end{equation}
このとき速度ベクトル $\mb{v}$ と磁場 $\mb{H}$ とは直交していることから,
\begin{equation*}
|\mb{v}\times\mb{H}|=vH\sin\pi/2=vH
\end{equation*}
よって, このときの放射強度 $I$ は次となる:
\begin{equation}
I=\frac{2e^{2}}{3c^{3}}\left(\frac{e}{mc}\right)^{2}|\mb{v}\times\mb{H}|^{2}=\frac{2e^{4}v^{2}H^{2}}{3m^{2}c^{5}}
\tag{53}
\end{equation}


の各成分の式は, 次の形に書ける:
