電磁気学の相対論的記述 part 3
以下は「ファインマン物理学」の第25章の第5節と第26章の第1節に多少の修正と加筆をしたものである．ここでは $c=1$ とする．
動く電荷による４元ポテンシャル
$ \def\BK#1#2{\langle #1|#2\rangle} \def\ppdiff#1#2{\frac{\partial #1}{\partial #2}} \def\odiff#1{\frac{d}{d #1}} \def\pdiff#1{\frac{\partial}{\partial #1}} \def\Bppdiff#1#2{\frac{\partial^{2}#1}{\partial #2^{2}}} \def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}} \def\mb#1{\mathbf{#1}} \def\ds#1{\mbox{${\displaystyle\strut #1}$}} $ 既に述べたことの中に事実上含まれている (implicit in) ことではあるが, 運動している系に於ける $\phi$ と $\mb{A}$ を, 静止している系の $\phi$ と $\mb{A}$ で与える変換則を書き下して見よう．$A_{\mu}=(\phi,\mb{A})$ は４ベクトルなので,変換の式はちょうど式(25.1)と同じやり方のものであるべきである．ただし, $t$ は $\phi$ で, そして$\mb{x}$ は $\mb{A}$ で置き換える．従って,
\begin{equation}
\phi^{'}=\frac{\phi-vA_x}{\sqrt{1-v^{2}}},\quad \quad A^{'}_{x}=\frac{A_x-v\phi}{\sqrt{1-v^{2}}},
\quad A^{'}_{y}=A_{y},\quad A^{'}_{z}=A_{z}
\tag{25.24}
\end{equation}
これはダッシュの付いていない座標系 $S$ で観測されることであるが,「ダッシュの付いた座標系 $S^{'}$ は正の $x$ 方向に速さ $v$ で運動していること」を仮定している．
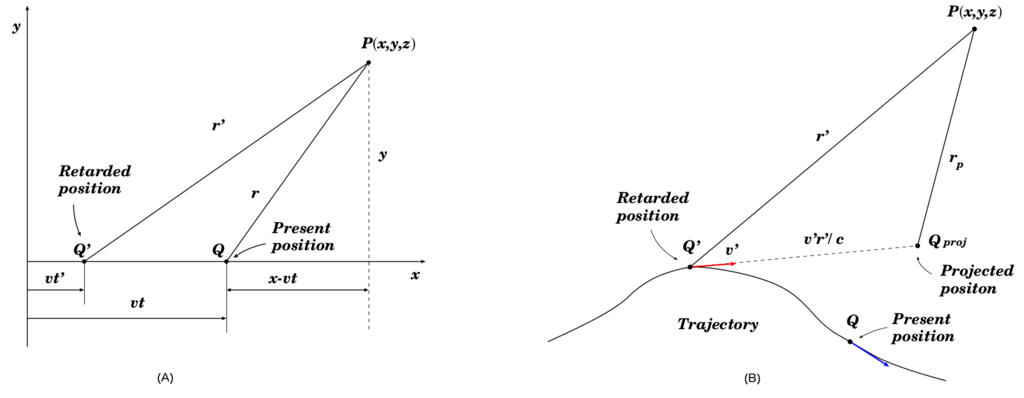
前のブログ：「Liénard-Wiechert の点ポテンシャルについて」で, 直線上を一定な速さ (uniform velocity) で運動する電荷の場がリエナール・ヴィーヒェルトのポテンシャルになることを見た．４ベクトル $A_{\mu}$ の有益な一例として, 再度それを相対論的に求めて見よう．$x$ 軸に沿って速さ $v$ で運動している電荷 $q$ のベクトルポテンシャル及びスカラーポテンシャルはどれくらいであろうか (what)？．この問題は, 電荷と共に運動する座標系では簡単である．なぜなら, その座標系では電荷は静止したままだからである．上図に示すように, 電荷は $S^{'}$ 系の原点に在ると仮定しよう (Let's say that)．すると運動している系に於けるスカラーポテンシャルは次で与えられる：
\begin{equation}
\phi^{'}=\frac{q}{r^{'}},
\tag{25.25}
\end{equation}
ただし $r^{'}$ は, 動いている系で測定したときの電荷 $q$ から場の点 $P$ までの距離である．ベクトルポテンシャル $\mb{A}^{'}$ はもちろんゼロである．
すると今や, 静止座標系で測定されるポテンシャル $\phi$ と $\mb{A}$ を求めることは容易である (it is straightforward to find)．式 (25.24) の逆関係は次である：
\begin{equation}
\phi=\frac{\phi^{'}+vA^{'}_x}{\sqrt{1-v^{2}}},\quad \quad A_{x}=\frac{A^{'}_x+v\phi^{'}}{\sqrt{1-v^{2}}},
\quad A_{y}=A^{'}_{y},\quad A_{z}=A^{'}_{z}
\tag{25.26}
\end{equation}
これに, 式 (25.25) で与えられている $\phi^{'}$ と $\mb{A}^{'}=0$ を用いると次を得る：
\begin{equation*}
\phi=\frac{q}{r^{'}\sqrt{1-v^{2}}}=\frac{q}{\sqrt{1-v^{2}}\sqrt{x^{' 2}+y^{' 2}+z^{' 2}}}
\end{equation*}
これが $S$ で見たスカラーポテンシャル $\phi$ である．しかし, 残念なことに, 上式は $S^{'}$ 座標系で表現されている． $S$ の量 $(t,x,y,z)$ で表現したものは, 式 (25.1) を用いて $(t^{'},x^{'},y^{'},z^{'})$ を置き換えることで (by substituting) 得ることが出来て, 次となる：
\begin{equation}
\phi=\frac{1}{\sqrt{1-v^{2}}}\frac{q}{\ds{\left[\frac{(x-vt)^{2}}{1-v^{2}}+y^{2}+z^{2}\right]^{1/2}}}
\tag{25.27}
\end{equation}
$\mb{A}$ の成分は上と同じ手続きに従えばよく, 次を示すことが出来る：
\begin{equation}
\mb{A}=\mb{v}\phi=(v\phi,0,0),\quad \text{or}\quad
A_x=\frac{1}{\sqrt{1-v^{2}}}\frac{qv}{\ds{\left[\frac{(x-vt)^{2}}{1-v^{2}}+y^{2}+z^{2}\right]^{1/2}}},\quad
A_y=A_z=0
\tag{25.28}
\end{equation}
これらの公式は, 第21章で (前のブログで) 別のやり方により導出したリエナール・ヴィーヒェルトのポテンシャル式 (20.39) と同じである．ただし, それは $c=1$ とはしない表式である．
動く電荷の４元ポテンシャル
前章の式 (25.7) と式 (25.8) は時間 $t$ に於ける位置 $P=(x,y,z)$ でのポテンシャルを与える式であるが, それは「現在の位置」(それは時刻 $t$ での位置という意味である) が $x=vt$ に在る電荷が作るポテンシャルの式である．
\begin{align*}
\phi&=\frac{q}{\sqrt{1-v^{2}}}\frac{1}{\ds{\sqrt{\left(\frac{x-vt}{\sqrt{1-v^{2}}}\right)^{2}+y^{2}+z^{2}}}},\\
A_x&=\frac{\mb{v}q}{\sqrt{1-v^{2}}}
\frac{1}{\ds{\sqrt{\left(\frac{x-vt}{\sqrt{1-v^{2}}}\right)^{2}+y^{2}+z^{2}}}},\quad
A_y=A_z=0.
\tag{26.1}
\end{align*}
これらの式は, 動いている電荷の 「現在位置 」$Q$ から測定した座標値 $(x-vt)$, $y$, $z$ によって表わされていることに注意すべし．しかし我々が知る実際の影響は, 実は速さ $c$ で移動している．よって本当に大事なのは, 遅延点 $Q^{'}$まで戻った位置での電荷の振舞いである．点 $Q^{'}$ は $x=vt^{'}$ に在る ( ただし $t^{'}=t-r^{'}/c$ は遅延時刻である )．しかし電荷は直線上を一定速度で動いていると述べた．よって当然ながら $Q^{'}$ での振舞いと現在位置 $Q$ とは直接的な関連性を持っている．実際, ポテンシャルは遅延時刻 $t^{'}$ に於ける電荷の位置 $Q^{'}$ と速度 $v^{'}$ のみに依存するという仮定を付け加えるならば, 式 (26.1) は任意な仕方で運動する電荷に対するポテンシャルの完全な公式となる．それは次のような具合である (It works this way)．電荷がある任意な仕方で, 例えば下図 (B) のような軌道を描いて運動しているとしよう．そして点 $P=(x,y,z)$ でのポテンシャルを見つけようとしている．まずは, その点に対する遅延位置 $Q^{'}$ と速度 $v^{'}$ を求める．次に電荷は遅延時間 $(t^{'}-t)$ の間だけその速度で運動し続けると仮定し(imagine), 電荷は仮想の点 $Q_{\text{proj}}$ に出現するとする．それは「投影点」(projected position) と呼ぶことができ, そこには速さ $v^{'}$ で到達するとする．( 実際の電荷は勿論そんなことはしない．$t$ での実際の位置は $Q$ である! )．このとき, 位置 $P=(x,y,z)$ でのポテンシャルはちょうど, 投影点 $Q^{'}$ に於ける仮想電荷に対して式 (26.1) が与える値となる．言いたいのは, 「ポテンシャルは遅延時刻で電荷が行っていることだけに依存する」という事である．すなわち, 時刻 $t$ に観測点 $P=(x,y,z)$ に出現するポテンシャルが既に決定された後, 電荷が一定速度で運動し続けようが時刻 $t^{'}$ の後で速度を変えようが (それには無関係で), ポテンシャルの値は同じであるという事である．
任意の運動をする一つの電荷からのポテンシャルの公式を得たとき, 我々は当然ながら完全な電気力学を得たことになる．なぜなら,重ね合わせの原理により, どんな任意分布する電荷のポテンシャルでも計算できるからである．従って, 電気力学の全ての現象を総括するには, マクスウェル方程式を書き下すか, あるいは次のような一連の注意点に従うことで実行できる．( それらは, いつか砂漠の島に行く場合に備えて覚えておいてほしい．全ては,それらから再構築出来るからだ．当然ながらローレンツ変換は知っているべきだ．砂漠の島や他のどんな場所に居てもそれは決して忘れてはいけない [ Remember them in case you are ever on a desert island. From them, all can be reconstructed. You will, of course, know the Lorentz transformation; you will never forget that on a desert island or anywhere else.] )．
( 注意 ) 上の英文の部分は訳本と違ってしまっているので, 学生さんは英文を自分なりに読んで解釈し直して下さい．
第一に, $A_{\mu}$は４ベクトルであること．第二に, 静止している電荷のクーロンポテンシャルは $q/r$ であること．そして第三に, 任意に運動する一つの電荷によって作られるポテンシャルは遅延時刻に於けるその速度と位置だけに依存することである．これら３つの事実から全てが得られる (With those three facts we have everything)．$A_{\mu}$ が４ベクトルであるという事実から, 既知であるクーロンポテンシャルを変換することで一定速度の場合のポテンシャルが得られる． 更にまた「ポテンシャルは遅延時刻に於ける過去の速度にのみ依存する」という前の記述から, ポテンシャルを見出すのに投影位置を見出す手法 (game) を利用することが出来る．以上のやり方は, 物事を行うのに特に有用だという訳ではない．しかし,「物理学の法則は,非常に多くの異なる仕方で説明できること」を示せるのは面白いことだ．
軽率な人たちは, ときどき「電気力学の全てはローレンツ変換とクーロンの法則だけから導出できる」と言う．勿論だが, それは完全な間違いである．まず, 我々は「スカラーポテンシャルとベクトルポテンシャルが存在し, それらが４ベクトルを形成する」ことを仮定しなければならない．それにより, ポテンシャルがどのような変換をするのかが分かるのである． その場合に, なぜ遅延時刻での影響だけが重要なことなのであろうか？．更にまた, なぜポテンシャルは位置と速度だけに依存するのであろうか？．そして, 例えば, 加速度にはなぜ依存しないのであろうか？．「場 $\mb{E}$ と $\mb{H}$」は加速度にも依存する！．もしそれらの場についてポテンシャルと同様な議論をしようとするならば,「場は遅延時刻に於ける位置と速度にのみ依存する」ということになるだろう．しかし, もしそうなら加速度運動している電荷を考えたとき, その電荷が作る場は投影位置に於ける電荷による場と同じ (すなわち位置と速度だけに依存し加速度には依らない場) になるはずである．しかし事実はそうでない！．「場 $\mb{E}$ と $\mb{H}$」は経路に沿った位置と速度にだけでなく, その加速度にも依存する！のであった．従って,「ローレンツ変換からは全てが導出できる」というこの偉大な言説には, 幾つかの付加的な暗黙の前提 (tacit assumptions) が存在しているのである．(この場合には,「ポテンシャル $A_{\mu}$ が４ベクトルを形成すること」,「ポテンシャルは位置と速度だけに依存すること」, そして「場は加速度にも依存すること」が暗黙の前提になっている)．非常に少ない前提から大量の事柄が導出できる包括的な言説を調べてみるときはいつも, それが誤りであることを見出すのが常である．十分に注意して考えると, たいていは決して明瞭ではない隠れた仮定が非常に多く存在するのである．(Whenever you see a sweeping statement that a tremendous amount can come from a very small number of assumptions, you always find that it is false. There are usually a large number of implied assumptions that are far from obvious if you think about them sufficiently carefully.)
